题目内容
5.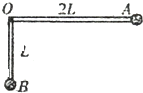 如图所示,质量分别为2m和3m的两个小球同定在一根直角尺的两端A、B,直角尺的定点O处 有光滑的固定转动轴,AO,BO的长分别为2L和L,开始时直角尺的AO部分处于水平位置而B在O的正下方,让该系统由静止开始自由转动,(不计直角尺质量),则下列说法正确的是( )
如图所示,质量分别为2m和3m的两个小球同定在一根直角尺的两端A、B,直角尺的定点O处 有光滑的固定转动轴,AO,BO的长分别为2L和L,开始时直角尺的AO部分处于水平位置而B在O的正下方,让该系统由静止开始自由转动,(不计直角尺质量),则下列说法正确的是( )| A. | B球能摆到的最大高度与O点同一水平面 | |
| B. | 当A球经过最低点时速度为2$\sqrt{gl}$ | |
| C. | 当A球经过最低点时杆对A的拉力等于A的重力 | |
| D. | B球能上升的最大的高度为$\frac{32L}{25}$ |
分析 (1)AB两个球组成的系统机械能守恒,根据系统的机械能守恒列式可以求得AB速度之间的关系,同时由于AB是同时转动的,它们的角速度的大小相同.联立即可求解v.
(2)B球不可能到达O的正上方,它到达最大高度时速度一定为零,再根据系统的机械能守恒求解最大高度h.
(3)由向心力公式求解A经最低点时的杆的作用力.
解答  解:以直角尺和两小球组成的系统为对象,由于转动过程不受摩擦和介质阻力,所以该系统的机械能守恒.
解:以直角尺和两小球组成的系统为对象,由于转动过程不受摩擦和介质阻力,所以该系统的机械能守恒.
A、B球不可能到达O的正上方,它到达最大高度时速度一定为零,设该位置位于OA杆竖直位置向左偏了α角.如图所示(2).则有
2mg•2Lcosα=3mgL(1+sinα)
此式可化简为 4cosα-3sinα=3
解得 sin(53°-α)=sin37°,α=16°
所以B球能上升的最大高度h=L+Lsin16°=L+Lsin(53°-37°)
解得h=1.28L;故A错误;D正确;
B、A、B转动的角速度始终相同,由v=ωr,有v=2vB
系统的机械能守恒,得:2mg•2L=3mg•L+$\frac{1}{2}•2m{v}^{2}$+$\frac{1}{2}•3m•{v}_{B}^{2}$
解得 v=$\sqrt{\frac{8gL}{11}}$;故B错误;
C、当A球经过最低点时,由向心力公式可知:
F-2mg=2m$\frac{{v}^{2}}{2L}$;
解得:F=2mg+$\frac{8mg}{11}$=$\frac{30mg}{11}$;故C错误;
故选:D.
点评 本题中的AB的位置关系并不是在一条直线上,所以在球AB的势能的变化时要注意它们之间的关系,在解题的过程中还要用到数学的三角函数的知识,要求学生的数学基本功要好,本题由一定的难度.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
16. 如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )
如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )
 如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )
如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )| A. | 原子核发生了α衰变 | B. | 原子核发生了β衰变 | ||
| C. | 原子核同时发生了α、β衰变 | D. | 该原子核放出一个中子 |
14. 如图所示,质量为m、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动.小物块和小车之间的摩擦力为Ff,小物块滑到小车的最右端时,小车运动的距离为x,在这个过程中,以下结论错误的是( )
如图所示,质量为m、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动.小物块和小车之间的摩擦力为Ff,小物块滑到小车的最右端时,小车运动的距离为x,在这个过程中,以下结论错误的是( )
 如图所示,质量为m、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动.小物块和小车之间的摩擦力为Ff,小物块滑到小车的最右端时,小车运动的距离为x,在这个过程中,以下结论错误的是( )
如图所示,质量为m、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动.小物块和小车之间的摩擦力为Ff,小物块滑到小车的最右端时,小车运动的距离为x,在这个过程中,以下结论错误的是( )| A. | 小物块到达小车最右端时,小车具有的动能为Ff•x | |
| B. | 小物块克服摩擦力所做的功为Ff(l+x) | |
| C. | 小物块和小车增加的机械能为F•x | |
| D. | 小物块到达小车最右端时具有的动能为(F-Ff)(l+x) |
15.下列物理量中,都是矢量的是( )
| A. | 力和速率 | B. | 加速度和力 | C. | 力和路程 | D. | 力和质量 |

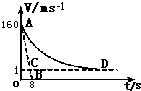 “神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问:
“神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问: 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PO,导轨足够长,间距为L,其电阻不计,导轨平面与磁场垂直,ab、cd为两根相同的、垂直于导轨水平放置的金属棒,电阻均为R,质量均为m,与金属导轨平行的水平细线一端固定,另一端与cd棒的中点连接,细线能承受的最大拉力为T,一开始细线处于伸直状态,ab棒在平行导轨的水平拉力的作用下以加速度a向右做匀加速直线运动,两根金属棒运动时始终与导轨接触良好且与导轨相垂直.
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PO,导轨足够长,间距为L,其电阻不计,导轨平面与磁场垂直,ab、cd为两根相同的、垂直于导轨水平放置的金属棒,电阻均为R,质量均为m,与金属导轨平行的水平细线一端固定,另一端与cd棒的中点连接,细线能承受的最大拉力为T,一开始细线处于伸直状态,ab棒在平行导轨的水平拉力的作用下以加速度a向右做匀加速直线运动,两根金属棒运动时始终与导轨接触良好且与导轨相垂直. 质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Tmax=46N,取g=10m/s2.试求:
质量m=1kg的小球在长为L=1m的细绳作用下在竖直平面内做圆周运动,细绳能承受的最大拉力Tmax=46N,取g=10m/s2.试求: