题目内容
20.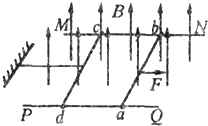 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PO,导轨足够长,间距为L,其电阻不计,导轨平面与磁场垂直,ab、cd为两根相同的、垂直于导轨水平放置的金属棒,电阻均为R,质量均为m,与金属导轨平行的水平细线一端固定,另一端与cd棒的中点连接,细线能承受的最大拉力为T,一开始细线处于伸直状态,ab棒在平行导轨的水平拉力的作用下以加速度a向右做匀加速直线运动,两根金属棒运动时始终与导轨接触良好且与导轨相垂直.
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中有两条光滑固定的平行金属导轨MN、PO,导轨足够长,间距为L,其电阻不计,导轨平面与磁场垂直,ab、cd为两根相同的、垂直于导轨水平放置的金属棒,电阻均为R,质量均为m,与金属导轨平行的水平细线一端固定,另一端与cd棒的中点连接,细线能承受的最大拉力为T,一开始细线处于伸直状态,ab棒在平行导轨的水平拉力的作用下以加速度a向右做匀加速直线运动,两根金属棒运动时始终与导轨接触良好且与导轨相垂直.(1)求经多长时间细线被拉断?
(2)求细线被拉断前,对ab棒的水平拉力随时间变化关系.
(3)若在细线被拉断瞬间撤去水平拉力,求此后电路中产生的焦耳热.
分析 (1)ab棒向右做匀加速运动进,穿过回路abcd的磁通量增大,回路中产生感应电动势和感应电流,cd受到向右的安培力作用,当安培力大小等于细线的最大拉力时,细线被拉断.根据 E=BLv、I=$\frac{E}{2R}$、F=BIL,v=at,推导出安培力F的表达式,根据根据F=T,即可求得时间t;
(2)对ab进行受力分析,由牛顿第二定律可求得水平拉力随时间的变化关系;
(3)根据系统动量守恒求得两棒匀速运动时的速度,根据能量守恒求解回路总共产生的焦耳热.
解答 解:(1)设绳被拉断时回路中的电流为I,设拉断时棒ab中电动势为E,速度为v,运动时间为t,则有
感应电动势 E=BLv
感应电流 I=$\frac{E}{2R}$
又 v=at
cd棒所受的安培力为 F安=BIL
联立解得,F安=$\frac{{B}^{2}{L}^{2}at}{2R}$
细线即将拉断时,对cd有:T=F安;
解得:t=$\frac{2TR}{a{B}^{2}{L}^{2}}$
(2)对ab棒受力分析可知:其受拉力与安培力的作用而做匀加速直线运动;
则有:Fab-$\frac{{B}^{2}{L}^{2}at}{2R}$=ma;
故Fab=$\frac{{B}^{2}{L}^{2}at}{2R}$+ma;
(3)在细线被拉断瞬间撤去水平拉力,设此后两棒匀速运动时的相同速度为v′,取向右为正方向,据系统的动量守恒得:
mv=2mv′
线断后回路中产生的焦耳热为
Q=$\frac{1}{2}$mv2-$\frac{1}{2}$×2mv2;
解得:Q=$\frac{m{T}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$
答:(1)经$\frac{2TR}{a{B}^{2}{L}^{2}}$时间细线被拉断.
(2)细线被拉断前,对ab棒的水平拉力随时间变化关系为Fab=$\frac{{B}^{2}{L}^{2}at}{2R}$+ma;
(3)若在细线被拉断瞬间撤去水平拉力,此后电路中产生的焦耳热为$\frac{m{T}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$.
点评 本题双杆模型,当cd棒不动时,只有ab棒切割磁感线产生感应电动势,关键要会推导安培力的表达式.当cd棒也运动时,关键要正确分析两棒的运动情况,根据动量守恒和能量守恒结合求解热量.

 一课一练课时达标系列答案
一课一练课时达标系列答案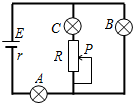 如图所示的电路,A、B、C为三个相同的灯泡,每一个灯泡的电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )
如图所示的电路,A、B、C为三个相同的灯泡,每一个灯泡的电阻大于电源内阻,当变阻器的滑动触头P向上移动时( )| A. | A灯变亮,B灯和C灯都变暗 | B. | A灯变亮,B灯变暗,C灯变亮 | ||
| C. | 电源释放的总电功率增大 | D. | 电源输出的电功率增大 |
| A. | 10W | B. | 100W | C. | 1kW | D. | 10kW |
 如图所示,木块A、B静止叠放在光滑水平面上,A的质量为m,B的质量为2m.现施水平力F拉B,A、B刚好不发生相对滑动,一起沿水平面运动.若改用水平力F′拉A,使A、B也保持相对静止,一起沿水平面运动,则F′不得超过( )
如图所示,木块A、B静止叠放在光滑水平面上,A的质量为m,B的质量为2m.现施水平力F拉B,A、B刚好不发生相对滑动,一起沿水平面运动.若改用水平力F′拉A,使A、B也保持相对静止,一起沿水平面运动,则F′不得超过( )| A. | 2F | B. | $\frac{1}{2}$F | C. | 3F | D. | $\frac{1}{3}$F |
 如图所示,质量分别为2m和3m的两个小球同定在一根直角尺的两端A、B,直角尺的定点O处 有光滑的固定转动轴,AO,BO的长分别为2L和L,开始时直角尺的AO部分处于水平位置而B在O的正下方,让该系统由静止开始自由转动,(不计直角尺质量),则下列说法正确的是( )
如图所示,质量分别为2m和3m的两个小球同定在一根直角尺的两端A、B,直角尺的定点O处 有光滑的固定转动轴,AO,BO的长分别为2L和L,开始时直角尺的AO部分处于水平位置而B在O的正下方,让该系统由静止开始自由转动,(不计直角尺质量),则下列说法正确的是( )| A. | B球能摆到的最大高度与O点同一水平面 | |
| B. | 当A球经过最低点时速度为2$\sqrt{gl}$ | |
| C. | 当A球经过最低点时杆对A的拉力等于A的重力 | |
| D. | B球能上升的最大的高度为$\frac{32L}{25}$ |
| A. | 物体做曲线运动,其速度一定改变 | |
| B. | 物体做曲线运动,其加速度一定改变 | |
| C. | 物体在恒力作用下运动,其速度方向一定不变 | |
| D. | 物体在变力作用下运动,其速度大小一定改变 |
| A. | 约里奥-居里夫妇发现人工放射性同位素的方程为${\;}_{13}^{27}$Al+${\;}_{2}^{4}$He→${\;}_{15}^{30}$P+${\;}_{0}^{1}$n | |
| B. | 卢瑟福发现中子的核反应方程为${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n | |
| C. | 查得威克发现质子的核反应方程为${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| D. | 贝克勒尔发现了天然放射现象,说明了原子核是有内部结构的 |
| A. | 障碍物的尺寸小于或等于波长时有明显的衍射现象 | |
| B. | 旋转振动的音叉听到的声音有强弱变化,属于波的干涉现象 | |
| C. | 受迫振动的频率等于物体的固有频率 | |
| D. | 受迫振动时,驱动力的频率与物体的固有频率相差越大振幅越小 |
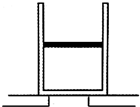 如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若保持温度不变将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2.求:
如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若保持温度不变将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2.求: