题目内容

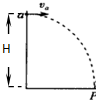
如图所示，在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球（可视为质点），最终它们分别落在圆弧上的A点和B点，已知OA与OB互相垂直，且OA与竖直方向成α角，则两小球初速度之比
v1
v2
为（　　）
A．tanαB．
cosα
sinα
C．tanα
tanα
D．
cosα
sinα

由几何关系可知，A的竖直位移hA=Rcosα，水平位移xA=Rsinα；
B的竖直位移hB=Rcos（90°-α）=Rsinα，水平位移xB=Rsin（90°-α）=Rcosα
由平抛运动的规律可知，h=
1
2
gt2
x=v0t
解得v0=x
g
2h

则
v1
v2
=
xA
xB
?
hB
hA
=tanα
tanα

故选C．
练习册系列答案
相关题目
如图，x轴在水平地面上，y轴竖直向上，在y轴上的P点分别沿x轴正方向和y轴正方向以相同大小的初速度抛出两个小球a和b，轨迹如图，不计空气阻力，若b上行的最大高度等于P点离地的高度，则从抛出到落地，有（　　）
A．a的运动时间是b的运动时间的（
2
-1）倍
B．a的位移大小是b的位移大小的
2
倍
C．a、b落地时的速度相同，因此动能一定相同
D．a、b落地时的速度不同，但动能一定相同
一同学做飞镖游戏，已知圆盘的直径为d，飞镖距圆盘为L，且对准圆盘上边缘的A点水平抛出，初速度为v0，飞镖抛出的同时，圆盘以垂直圆盘且过盘心O的水平轴匀速转动，角速度为ω．若飞镖恰好击中A点，则下列关系正确的是（　　）
A．d
v20
=L2g
B．v0=ω
d
2
C．ωL=π（1+2π）v0，（n=0，1，2，3，…）
D．dω2=gπ2（1+2n）2，n=（0，1，2，3…）
下列说法中正确的是（　　）
A．平抛运动是匀变速运动
B．平抛运动的时间由抛出时的高度和初速度的大小共同决定
C．匀速圆周运动的物体受到的合外力是恒力
D．做匀速圆周运动的物体线速度不变
关于平抛运动和匀速圆周运动，下列说法中正确的是（　　）
A．平抛运动是匀变速曲线运动
B．平抛运动速度随时间的变化是不均匀的
C．匀速圆周运动是线速度不变的圆周运动
D．做匀速圆周运动的物体所受外力的合力不做功
如图所示，在一竖直面内，小球a从距地面高度为H的点，以初速度va沿水平方向抛出，经时间t落到地面上的P点，若不计空气阻力，则（　　）
A．若va增加，H保持不变，则小球在空中的运动时间增加
B．若va增加，H保持不变，则小球在空中的运动时间不变
C．若H增加，va保持不变，则小球的落地点仍为P点
D．若H增加，va保持不变，则小球的落地点在P点左侧
关于平抛运动下列说法正确的是（　　）
A．因为轨迹是曲线，所以平抛运动是变加速运动
B．运动时间由下落高度和初速度共同决定
C．水平位移由初速度决定
D．运动时间由下落高度决定
如图所示，水平屋顶高H=5m，墙高h=3.75m，墙到房子的距离L=3.6m，墙外马路宽x=7.4m，小球从房顶水平飞出落在墙外的马路上，求小球离开房顶时的速度．（取g=10m/s2）
一个物体以初速度v0水平抛出，经过时间t，竖直方向速度大小也为v0，则t为（　　）
A．
v0
g
B．
2v0
g
C．
v0
2g
D．
3v0
g

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网