题目内容
19. 如图所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场B中,金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.
如图所示,固定于水平面上的金属框架abcd,处在竖直向下的匀强磁场B中,金属棒MN沿框架以速度v向右做匀速运动.框架的ab与dc平行,bc与ab、dc垂直.MN与bc的长度均为l,在运动过程中MN始终与bc平行,且与框架保持良好接触.(1)请根据法拉第电磁感应定律,推导金属棒MN中的感应电动势E的表达式;
(2)若金属框架只有bc有电阻且为R=2Ω,金属棒MN电阻为r=1Ω、B=1T、l=0.5m、v=2m/s时,求NM两端的电压UNM值.
分析 (1)先求出金属棒MN向右滑行的位移,得到回路磁通量的变化量△Φ,再由法拉第电磁感应定律求得E的表达式;
(2)由E=Blv求感应电动势,再由串联电路的分压规律求解电压UNM值.
解答  解:(1)如图1所示,在一小段时间△t内,金属棒MN的位移为:△x=v△t
解:(1)如图1所示,在一小段时间△t内,金属棒MN的位移为:△x=v△t
这个过程中面积的变化量:△S=l△x=lv△t
穿过闭合电路磁通量的变化量:△Φ=B△S=Blv△t
由法拉第电磁感应定律E=$\frac{△Φ}{△t}$ 可得E=Blv
(2)金属棒产生的感应电动势 E=Blv=1×0.5×2V=1V
根据右手定则判断知,M端的电势比N端的电势高,则
NM两端的电压 UNM=-$\frac{R}{R+r}$E=-$\frac{2}{3}$V
答:
(1)推导见上.
(2)NM两端的电压UNM为-$\frac{2}{3}$V.
点评 本题要掌握推导感应电动势E=BLv的方法,建立物理模型,理清思路是关键.

练习册系列答案
相关题目
10.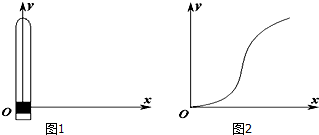 如图1所示是书本上演示小蜡块运劝规律的装置.在蜡块沿玻璃管(y方向)上升的同时,将玻璃管紧贴着黑板沿水平方向(x方向)向右运动,得到了蜡块相对于黑板(xoy平面)运动的轨迹图(图2).则蜡块沿玻璃管的上升运动与玻璃管沿水平方向的运动,可能的形式是( )
如图1所示是书本上演示小蜡块运劝规律的装置.在蜡块沿玻璃管(y方向)上升的同时,将玻璃管紧贴着黑板沿水平方向(x方向)向右运动,得到了蜡块相对于黑板(xoy平面)运动的轨迹图(图2).则蜡块沿玻璃管的上升运动与玻璃管沿水平方向的运动,可能的形式是( )
 如图1所示是书本上演示小蜡块运劝规律的装置.在蜡块沿玻璃管(y方向)上升的同时,将玻璃管紧贴着黑板沿水平方向(x方向)向右运动,得到了蜡块相对于黑板(xoy平面)运动的轨迹图(图2).则蜡块沿玻璃管的上升运动与玻璃管沿水平方向的运动,可能的形式是( )
如图1所示是书本上演示小蜡块运劝规律的装置.在蜡块沿玻璃管(y方向)上升的同时,将玻璃管紧贴着黑板沿水平方向(x方向)向右运动,得到了蜡块相对于黑板(xoy平面)运动的轨迹图(图2).则蜡块沿玻璃管的上升运动与玻璃管沿水平方向的运动,可能的形式是( )| A. | 小蜡块沿玻璃管做匀速直线运动,玻璃管沿水平方向先加速后减速 | |
| B. | 小蜡块沿玻璃管做匀速直线运动,玻璃管沿水平方向先减速后加速 | |
| C. | 小蜡块沿玻璃管做匀加速直线运动,玻璃管沿水平方向做匀加速直线运动 | |
| D. | 小蜡块沿玻璃管做匀加速直线运动,玻璃管沿水平方向做匀速直线运动 |
14.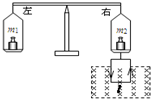 如图所示为“等臂电流天平”,可以用来测量匀强磁场的磁感应强度.它的右臂挂着一矩形线圈,设其匝数n=9,线圈的水平边长为l=0.10m,处在匀强磁场内,磁感应强度B的方向与线圈平面垂直.当线圈中通入如图方向的电流I=0.10A时,调节砝码使两臂平衡.然后使电流反向,大小不变,这时需要在左盘中增加质量为m=9.00g的砝码,才能使两臂再达到新的平衡.则磁感应强度B的大小为(g=10m/s2)( )
如图所示为“等臂电流天平”,可以用来测量匀强磁场的磁感应强度.它的右臂挂着一矩形线圈,设其匝数n=9,线圈的水平边长为l=0.10m,处在匀强磁场内,磁感应强度B的方向与线圈平面垂直.当线圈中通入如图方向的电流I=0.10A时,调节砝码使两臂平衡.然后使电流反向,大小不变,这时需要在左盘中增加质量为m=9.00g的砝码,才能使两臂再达到新的平衡.则磁感应强度B的大小为(g=10m/s2)( )
 如图所示为“等臂电流天平”,可以用来测量匀强磁场的磁感应强度.它的右臂挂着一矩形线圈,设其匝数n=9,线圈的水平边长为l=0.10m,处在匀强磁场内,磁感应强度B的方向与线圈平面垂直.当线圈中通入如图方向的电流I=0.10A时,调节砝码使两臂平衡.然后使电流反向,大小不变,这时需要在左盘中增加质量为m=9.00g的砝码,才能使两臂再达到新的平衡.则磁感应强度B的大小为(g=10m/s2)( )
如图所示为“等臂电流天平”,可以用来测量匀强磁场的磁感应强度.它的右臂挂着一矩形线圈,设其匝数n=9,线圈的水平边长为l=0.10m,处在匀强磁场内,磁感应强度B的方向与线圈平面垂直.当线圈中通入如图方向的电流I=0.10A时,调节砝码使两臂平衡.然后使电流反向,大小不变,这时需要在左盘中增加质量为m=9.00g的砝码,才能使两臂再达到新的平衡.则磁感应强度B的大小为(g=10m/s2)( )| A. | 0.45T | B. | 0.5T | C. | 0.9T | D. | 1T |
4.“空间站”是科学家进行天文探测和科学实验的特殊而又重要的场所,假设“空间站”正在地球赤道平面内的圆轨道上运行,其离地球表面的高度为同步卫星离地球表面高度的十分之一,且运行方向与地球自转方向一致.下列说法正确的是( )
| A. | “空间站”运行的速度等于同步卫星运行速度的$\sqrt{10}$倍 | |
| B. | “空间站”运行的加速度大于同步卫星运行的加速度 | |
| C. | 站在地球赤道上的人观察到“空间站”静止不动 | |
| D. | 在“空间站”工作的宇航员因不受重力而在舱中悬浮或静止 |
7.大型游轮在海上航行时根据《1974年海上人命公约》及1983修正案中相关规定,船上要配备救生艇.如图1所示是我国某科研机构自主研制的自由抛落全封闭救生艇.如表是一型号救生艇的尺寸.
灾难来临时,为了保证安全,要求救生艇能在几秒钟内从船上脱离并逃离大型船舶下沉时形成的巨大的海面漩涡,为此需要试验此救生艇能否从50m高度的游轮上面抛出后平稳跃升到水面迅速离开.设某次实验时救生艇恰好沿着南北方向,面向南方,沿着和水平成600角的斜面由静止开始加速运动,斜面一直延伸到水面,斜面和救生艇底部不计摩擦,假设在这一位置地磁场恰好垂直此斜面.如图,试验艇为玻璃钢制成,艇内壁恰好有U型导线通过艇内部地面延伸到两侧面最宽处,救生艇落海瞬间左右两侧导线端点间的电动势为1.5mv.方便计算艇宽取作$\sqrt{10}$m,g=10m/s2.求此处地磁场的磁感应强度B.(结果保留一位有效数字)

| 型号 | 计算长度 | 艇宽 | 总高 | 额定乘员 | 总重量 |
| 6.0FF 耐火型 | 6.00m | 3.16m | 3.24m | 22-26人 | 5130KG |

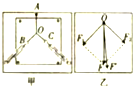 “探究力的平行四边形定则”的实验如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细线的结点,OB和OC为细绳,图乙所示是在白纸上根据实验结果画出的图,F′为用一个弹簧测力计所测得的结果
“探究力的平行四边形定则”的实验如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细线的结点,OB和OC为细绳,图乙所示是在白纸上根据实验结果画出的图,F′为用一个弹簧测力计所测得的结果
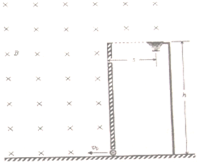 如图所示,水平地面上方有一底部带有小孔的绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及板上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电量q=-1×10-3C、直径略小于小孔宽度的带电小球(视为质点),以某一速度垂直于磁场方向从小孔水平射入,恰好做匀速圆周运动,若与档板相碰就以原速率弹回,且不计碰撞时间,碰撞时小球的电量保持不变,取g=10m/s2,求:
如图所示,水平地面上方有一底部带有小孔的绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及板上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电量q=-1×10-3C、直径略小于小孔宽度的带电小球(视为质点),以某一速度垂直于磁场方向从小孔水平射入,恰好做匀速圆周运动,若与档板相碰就以原速率弹回,且不计碰撞时间,碰撞时小球的电量保持不变,取g=10m/s2,求: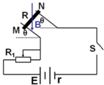 如图所示,两平行光滑金属导轨相距为0.2m,处于一匀强磁场中.金属棒MN的质量为m=0.01kg,电阻为R=8Ω,水平放置在导轨上接触良好.匀强磁场的磁感应强度B的大小为0.8T,方向竖直向下.电源的电动势E=10V,内阻r=1Ω.当开关S闭合时,MN处于静止状态.(θ=45°,g=10m/s2)求:
如图所示,两平行光滑金属导轨相距为0.2m,处于一匀强磁场中.金属棒MN的质量为m=0.01kg,电阻为R=8Ω,水平放置在导轨上接触良好.匀强磁场的磁感应强度B的大小为0.8T,方向竖直向下.电源的电动势E=10V,内阻r=1Ω.当开关S闭合时,MN处于静止状态.(θ=45°,g=10m/s2)求: