题目内容
20.甲、乙两船在平静的湖面上以相同的速度匀速航行,且甲船在前乙船在后,从甲船上相对于甲船的速度v,水平向后方的乙船上抛一沙袋,其质量为m,设甲船和沙袋总质量为M,乙船的质量也为M,向乙船抛沙袋后,甲、乙两船的速度变化多少?分析 沙袋与甲船组成的系统水平方向动量守恒,沙袋与乙船组成的系统在水平方向动量守恒,应用动量守恒定律求出甲、乙两船的速度,然后求出速度的变化.
解答 解:设甲乙两船的初速度为:v0,以甲船初速度方向为正方向,甲船与沙袋组成的系统在抛出沙袋过程中系统动量守恒,由动量守恒定律得:
Mv0=(M-m)v甲+m(v甲-v),
取沙袋和乙船为研究对象,系统动量守恒,由动量守恒定律得:
Mv0+m(v甲-v)=(M+m)v乙,
解得:v甲=v0+$\frac{m}{M}$v,v乙=v0-$\frac{m(M-m)}{M(M+m)}$v,
甲、乙两船的速度变化分别为:
△v甲=v甲-v0=$\frac{m}{M}$v,
△v乙=v乙-v0=-$\frac{m(M-m)}{M(M+m)}$v;
答:甲、乙两船的速度变化分别为$\frac{m}{M}$v、-$\frac{m(M-m)}{M(M+m)}$v.
点评 本题考查了求船的速度变化,分析清楚运动过程,正确选择研究对象,应用动量守恒定律即可正确解题,解题时注意个物体的速度应该是相对于同一参考系的速度.

练习册系列答案
相关题目
10.在下列情况下机械能不守恒的有( )
| A. | 在空气中匀速下落的降落伞 | |
| B. | 沿光滑圆弧面下滑的小球 | |
| C. | 在空中做斜抛运动的铅球(不计空气阻力) | |
| D. | 物体以8m/S2加速下落 |
11.北斗卫星导航系统是我国自行研制开发的区域性三维卫星定位与通信系统(CNSS),建成后的北斗卫星导航系统包括5颗同步卫星和30颗一般轨道卫星.对于其中的5颗同步卫星,下列说法中正确的是( )
| A. | 它们一定具有相同引力势能 | |
| B. | 一定位于空间同一轨道上 | |
| C. | 它们运行的加速度一定相同 | |
| D. | 它们运行的线速度一定不小于7.9km/s |
8.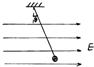 如图所示,悬线下挂着一个带正电的小球,它的质量为m、电量为q,整个装置处于水平向右的匀强电场中,电场强度为E.则下列说法中正确的是( )
如图所示,悬线下挂着一个带正电的小球,它的质量为m、电量为q,整个装置处于水平向右的匀强电场中,电场强度为E.则下列说法中正确的是( )
 如图所示,悬线下挂着一个带正电的小球,它的质量为m、电量为q,整个装置处于水平向右的匀强电场中,电场强度为E.则下列说法中正确的是( )
如图所示,悬线下挂着一个带正电的小球,它的质量为m、电量为q,整个装置处于水平向右的匀强电场中,电场强度为E.则下列说法中正确的是( )| A. | 小球平衡时,悬线上的拉力小于电场力 | |
| B. | 若剪断悬线,则小球作曲线运动 | |
| C. | 若剪断悬线,则小球作匀速运动 | |
| D. | 若剪断悬线,则小球作匀加速直线运动 |
4.一木块静止在光滑的水平面上,被水平飞来的子弹击中后移动了s时子弹与木块具有共同速度,子弹进入木块的深度为d,设木块对子弹的阻力恒定为F,则( )
| A. | 子弹原有的动能全部转化为子弹和木块的内能 | |
| B. | 子弹损失的动能等于子弹克服阻力所做的功,即F(d+s) | |
| C. | 木块与子弹组成的系统产生的热能为Q=Fs | |
| D. | 子弹击中木块后,木块一直做匀加速运动 |
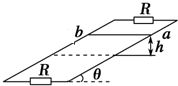 如图所示,两根足够长的固定的平行金属导轨位于倾角θ=30°的斜面上,导轨上、下端各接有阻值R=10Ω的电阻,导轨自身电阻忽略不计,导轨宽度L=2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=0.5T,质量为m=0.1kg,电阻r=5Ω的金属棒ab在较高处由静止释放,金属棒ab在下滑过程中始终与导轨垂直且与导轨接触良好,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s.(g=10m/s2),求:
如图所示,两根足够长的固定的平行金属导轨位于倾角θ=30°的斜面上,导轨上、下端各接有阻值R=10Ω的电阻,导轨自身电阻忽略不计,导轨宽度L=2m,在整个导轨平面内都有垂直于导轨平面向上的匀强磁场,磁感应强度B=0.5T,质量为m=0.1kg,电阻r=5Ω的金属棒ab在较高处由静止释放,金属棒ab在下滑过程中始终与导轨垂直且与导轨接触良好,当金属棒ab下滑高度h=3m时,速度恰好达到最大值v=2m/s.(g=10m/s2),求: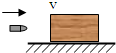 如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.
如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.