题目内容
3. 如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.
如图所示,质量为1kg的铜块静止于光滑的水平面上,一颗质量为50g的子弹以1000m/s的速度碰到铜块后,又以800m/s的速度被弹回,则此过程中铜块获得的速度大小为90m/s,子弹动量变化量的大小为90kg•m/s.
分析 子弹与铜块组成的系统动量守恒,由动量守恒定律可以求出铜块获得的速度,应用动量的定义式可以求出子弹动量的变化量大小.
解答 解:子弹与铜块组成的系统动量守恒,以子弹的初速度方向为正方向,
由动量守恒定律得:m1v0=m1v1+m2v2,
即:0.050×1000=0.050×(-800)+1×v2,
解得:v2=90m/s;
子弹动量的变化:
△p=m1v1-m1v0=0.050×(-800)-0.050×1000=-90kg•m/s,
动量变化量大小为90kg•m/s,负号表示:动量变化的方向:水平向左.
故答案为:90;90.
点评 本题考查了求滑块获得的速度,应用动量守恒定律即可正确解题,应用动量守恒定律解题时,要注意正方向的选择,否则会出错.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
19. 随着地球资源的日益匮乏和环境的日益恶劣,人类设想在地球远地轨道上建立一个未来的圆环形太空城.远远看去,好像一个巨大的车轮,圆环形的直径为D,“轮胎”是一个空心的大圆环,其内部直径为d(D>d),是太空城的生活区.同时,太空城还绕着自己的中心轴慢慢旋转,利用旋转时产生的离心效应而制造出人造重力,生活在其中的人类就有脚踏实地的感觉.已知地球半径R,表面重力加速度为g,地球自转周期为T,空间站轨道半径r.下列说法中正确的是( )
随着地球资源的日益匮乏和环境的日益恶劣,人类设想在地球远地轨道上建立一个未来的圆环形太空城.远远看去,好像一个巨大的车轮,圆环形的直径为D,“轮胎”是一个空心的大圆环,其内部直径为d(D>d),是太空城的生活区.同时,太空城还绕着自己的中心轴慢慢旋转,利用旋转时产生的离心效应而制造出人造重力,生活在其中的人类就有脚踏实地的感觉.已知地球半径R,表面重力加速度为g,地球自转周期为T,空间站轨道半径r.下列说法中正确的是( )
 随着地球资源的日益匮乏和环境的日益恶劣,人类设想在地球远地轨道上建立一个未来的圆环形太空城.远远看去,好像一个巨大的车轮,圆环形的直径为D,“轮胎”是一个空心的大圆环,其内部直径为d(D>d),是太空城的生活区.同时,太空城还绕着自己的中心轴慢慢旋转,利用旋转时产生的离心效应而制造出人造重力,生活在其中的人类就有脚踏实地的感觉.已知地球半径R,表面重力加速度为g,地球自转周期为T,空间站轨道半径r.下列说法中正确的是( )
随着地球资源的日益匮乏和环境的日益恶劣,人类设想在地球远地轨道上建立一个未来的圆环形太空城.远远看去,好像一个巨大的车轮,圆环形的直径为D,“轮胎”是一个空心的大圆环,其内部直径为d(D>d),是太空城的生活区.同时,太空城还绕着自己的中心轴慢慢旋转,利用旋转时产生的离心效应而制造出人造重力,生活在其中的人类就有脚踏实地的感觉.已知地球半径R,表面重力加速度为g,地球自转周期为T,空间站轨道半径r.下列说法中正确的是( )| A. | 太空城中的“地面”在图示的下表面 | |
| B. | 当太空城稳定地转动时,若在“生活区”上空某处静止释放一个物体,让太空城里的你来观察,你会观察到物体沿径向垂直太空城内边缘加速下落 | |
| C. | 若忽略太空城的自转,则太空城的绕地球转动的周期为$\sqrt{\frac{{r}^{3}{T}^{2}}{{R}^{3}}}$ | |
| D. | 若太空城的转速刚能提供和地球表面的实际重力加速度效果相同的人造“重力”,那么太空城自转的角速度为$\sqrt{\frac{2g}{D}}$ |
17.下列说法正确的是( )
| A. | 气体的内能是气体内所有分子热运动的动能和分子的势能的总和 | |
| B. | 气体的温度变化时,其分子的平均动能和分子的势能也随之改变 | |
| C. | 功不可以全部转化为热量,热能也不能全部转化为功 | |
| D. | 一定量的气体,在体积不变时,分子每秒平均碰撞器壁的次数随着温度的降低而减小 | |
| E. | 对于某一晶体,它可能没有规则的几何形状,但一定有固定的熔点 |
15. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )| A. | 小球的加速度在ab段不变,在bc段逐渐减小 | |
| B. | 小球的重力势能减少 | |
| C. | 小球在b点时速度最大 | |
| D. | 小球的机械能守恒 |
12. 如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
 如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )| A. | $\frac{fLm}{M+m}$ | B. | MgLcosθ | C. | 0 | D. | $\frac{1}{2}$mgLsin2θ |
13.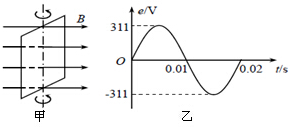 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )| A. | t=0.015s时穿过线框的磁通量变化率为零 | |
| B. | t=0.01s时线框平面与中性面重合 | |
| C. | 线框产生的交变电动势有效值为311V | |
| D. | 线框产生的交变电动势频率为100Hz |
 甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度?
甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度? 如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中A为阳极,K为阴极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数.若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数为6.0V,则光电管阴极材料的逸出功为4.5eV.现保持滑片P位置不变,若用光子能量为12eV的光照射阴极K,光电子的最大初动能增大.(填“增大”、“减小”、“不变”)
如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中A为阳极,K为阴极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数.若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数为6.0V,则光电管阴极材料的逸出功为4.5eV.现保持滑片P位置不变,若用光子能量为12eV的光照射阴极K,光电子的最大初动能增大.(填“增大”、“减小”、“不变”)