题目内容
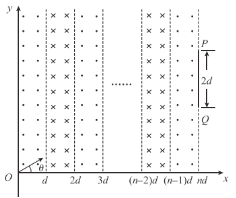
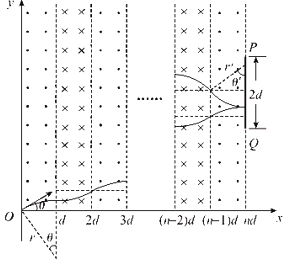
【题目】如图所示，在坐标系xOy的第一象限中存在n(n为奇数)个宽度均为d、磁感应强度大小均为B的匀强磁场，各磁场区域紧密连接，且左、右两侧边界相互平行，第1个磁场区域的左边界为y轴，磁场方向垂直纸面向外，相邻磁场区域的磁场方向相反。在第n个磁场区域的右边界上有一长为2d的探测板PQ，探测板的下边缘Q与x轴相距2.2d。坐标原点O处的粒子源以某一特定速度在xOy平面内不断向磁场区域发射质量为m，电荷量为+q的粒子，方向与x轴正方向成θ=30°角，每秒发射粒子的总数为N0，通过改变粒子发射速度的大小，可以使粒子从不同位置射出磁场。已知sin53°=0.8，cos53°=0.6，
=1.73，不计粒子重力且忽略粒子间的相互作用。
(1)若粒子从(d，0)点射出磁场，求粒子发射速度大小v1；
(2)若粒子均垂直打到探测板上并全部被反向弹回，且弹回速度大小为打板前速度大小的
，求：
I.探测板受到的平均作用力大小；
Ⅱ.n的所有可能值，并求出n取最大值时，粒子在磁场中运动的总时间t。(不计粒子与探测板发生碰撞的时间)
【答案】（1）
（2）（i） 
(ii)n的可能值有9、11、13、15，
【解析】
（1）由几何关系可知
，由牛顿第二定律可得
，故
；
（2）若粒子垂直打到板上，由粒子轨迹的对称性可知，粒子必定垂直经过第一个磁场区域的右边界，如图所示，由几何关系可得粒子在磁场中运动的半径为
I、同理可得粒子射入磁场的速度为
，故粒子被板弹回时的速度为
；
取一小段时间
，由动量定理可得
；
根据牛顿第三定律，探测板受到的平均作用力
；
II、粒子从O点出发至打到板上的过程中，沿y轴方向的位移
由题意可知
，解得
；
因为n为奇数，所以n的可能值为9、11、13、15；
当n=15时，可求得粒子被板弹回后在磁场中运动的半径为
；
设粒子被板弹回后在每个磁场区域中的运动轨迹所对应的圆心角为
，
所以
；
粒子在磁场中做圆周运动的周期
，与粒子速度大小无关，所以粒子在磁场中运动的总时间
；
