题目内容

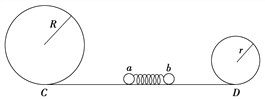
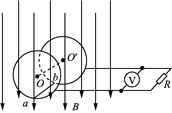
【题目】如图所示，水平光滑的绝缘细管中，两相同的带电金属小球相向运动，当相距L时，加速度大小均为a，速度大小均为v，相互作用力大小为F，已知A球带电荷量为+q，B球带电荷量为-3q，两球相碰后分开，则下列有关说法正确的是

A. 两球相碰位置为L的中点

B. 当两球相碰后再次相互L时，两球间相互作用力大小为F

C. 当两球相碰后再次相互为L时，两球加速度大小均为a

D. 当两球相碰后再次相互L时，两球速度大小均为v

【答案】A

【解析】A、碰撞前间距为L时,两球间的库仑力相等，金属球质量相同，所以加速度也相等，根据运动情况两个球应该同时运动中点相碰，故A正确；

BC、碰前相距为L时受到的库仑力为：

碰撞时电荷量先中和后均分，所以带电荷量都为-q，此时的库仑力为

，则加速度，故BC错误

D、碰后的库仑力小于碰前的库仑力，所以分开运动过程中库仑力做功小于碰前库仑力做功，所以当两球相碰后再次相距L时，两球速度大小均小于v，故D错误；

故选A

练习册系列答案
相关题目

【题目】在测量一节干电池的电动势和内阻的实验中，实验电路图如图所示，实验室提供下列器材：

电流表（量程0.6A，内阻约l.0Ω）

电压表V（量程3V，内阻约3kΩ）

滑动变阻器（0~20Ω）

滑动变阻器（0~2000Ω）

干电池E（电动势约1.5V，内阻未知）

开关及导线若干

（1）实验中滑动变阻器应选_____（填器材的代号）；

（2）实验时，改变滑动变阻器的阻值，得到两组测量数据和，则电源的电动势E＝___，内阻r= __；

（3）若有相同型号的新、旧两节干电池，分别接入图示电路，当电流在相同范围内变化时，接入旧干电池（电动势较小，内阻较大）时电压表读数变化范围__（填“一定大于”、“一定小于”或“可能等于”）接入新干电池时电压表读数变化范围。

【题目】地球表面附近存在一个竖直向下的电场，其大小约为100V/m。在该电场的作用下，大气中正离子向下运动，负离子向上运动，从而形成较为稳定的电流，这叫做晴天地空电流。地表附近某处地空电流虽然微弱，但全球地空电流的总电流强度很大，约为1800A。以下分析问题时假设地空电流在全球各处均匀分布。

（1）请问地表附近从高处到低处电势升高还是降低？

（2）如果认为此电场是由地球表面均匀分布的负电荷产生的，且已知电荷均匀分布的带电球面在球面外某处产生的场强相当于电荷全部集中在球心所产生的场强；地表附近电场的大小用E表示，地球半径用R表示，静电力常量用k表示，请写出地表所带电荷量的大小Q的表达式；

（3）取地球表面积S=5.1×1014m2，试计算地表附近空气的电阻率ρ0的大小；

（4）我们知道电流的周围会有磁场，那么全球均匀分布的地空电流是否会在地球表面形成磁场？如果会，说明方向；如果不会，说明理由。

【题目】a、b、c三个物体在同一条直线上运动，它们的位移一时间图像如图所示，其中a是一条顶点坐标为(0,10)的抛物线，下列说法正确的是（ ）

A. b、c两物体都做匀速直线运动，两个物体的速度相同

B. 在内,a、b两个物体间的距离逐渐变大

C. 物体c的速度越来越大

D. 物体a的加速度为

【题目】如图所示，劲度度系数的弹簧一端固定于地面上，另一端连接绝缘物体A，物体B置于A上不粘连，A不带电，B的带电量，A，B质量均为且都可看做质点，整个装置处于静止状态。物体B正上方有一带圆孔的挡板，质量为4kg的不带电绝缘物体C放于圆孔上方不掉落，现在挡板与地面之间加上竖直向上、大小的匀强电场使A、B开始运动，A、B分离时，A在某装置作用下迅速在该位量处于静止状态，以后此装量不再对A作用；A、B分离后，B向上运动并与C发生碰撞，且以后每次磁撞前C均已静止在圆孔上方，已知弹簧的弹性势能 (x为弹黄的形变量)，重力加速度为，B与A、C碰撞时为弹性碰撞且没有电荷转移。求：

(1)A、B两物体从开始运动到分离时上升的高度；

(2)A、B第一次碰后物体A向下运动的最大距离；

(3)从A、B第一次撞开始，A物体运动的总路程。

【题目】如图所示，半径分别为R＝1 m和r＝0.5 m的甲、乙两光滑圆轨道置于同一竖直平面内，两轨道之间由一段光滑水平轨道CD相连，在水平轨道CD上一轻弹簧被a、b两小球夹住，现同时由静止释放两小球，重力加速度取g＝10 m/s2.

①如果a、b小球都恰好能够通过各自圆轨道的最高点，求两小球的质量之比；

②如果a、b小球的质量均为0.5 kg，为保证两小球都能够通过各自圆轨道的最高点，求释放两小球前弹簧弹性势能的最小值．

【答案】(1) (2)

【解析】根据牛顿第二定律得出最高点的速度，根据机械能守恒定律，动量守恒定律列出等式求解；由动量守恒定律知两小球与弹簧分离时速度大小相等，再根据机械能守恒定律求解．

已知a、b小球恰好能通过各自圆轨道的最高点，则它们通过最高点时的速度大小分别为，

设两小球与弹簧分离时的速度大小分别为 ，根据动量守恒定律有

根据机械能守恒定律有，，。联立以上各式解得

②若ma=mb=0.5 kg，由动量守恒定律知两小球与弹簧分离时速度大小相等

当a小球恰好能通过最高点时，b小球一定也能通过最高点，a小球通过最高点的速度为，此时弹簧的弹性势能最小，最小值为

【点睛】解决该题关键能判断出小球能通过最高点的条件，然后根据动量守恒定律和机械能守恒定律联立列式求解。

【题型】解答题
【结束】
93

【题目】如图所示，在第一象限内有沿y轴负方向的电场强度大小为E的匀强电场．在第二象限中，半径为R的圆形区域内存在垂直纸面向外的匀强磁场，圆形区域与x、y轴分别相切于A、C两点．在A点正下方有一个粒子源P，P可以向x轴上方各个方向射出速度大小均为v0、质量为m、电荷量为＋q的带电粒子(重力不计，不计粒子间的相互作用)，其中沿y轴正向射出的带电粒子刚好从C点垂直于y轴进入电场．

(1)求匀强磁场的磁感应强度大小B.

(2)求带电粒子到达x轴时的横坐标范围和带电粒子到达x轴前运动时间的范围．

(3)如果将第一象限内的电场方向改为沿x轴负方向，分析带电粒子将从何处离开磁场，可以不写出过程．

【题目】磁流体发电机原理如图所示，等离子体高速喷射到加有强磁场的管道内，正、负离子在洛伦兹力作用下分别向A、B两金属板偏转，形成直流电源对外供电．则(　　)

A. 仅减小两板间的距离，发电机的电动势将增大

B. 仅增强磁感应强度，发电机的电动势将减小

C. 仅增加负载的阻值，发电机的输出功率将增大

D. 仅增大磁流体的喷射速度，发电机的总功率将增大

【题目】如图所示，水平导体棒ab质量为m、长为L、电阻为R0，其两个端点分别搭接在竖直平行放置的两光滑金属圆环上，两圆环半径均为r、电阻不计．阻值为R的电阻用导线与圆环相连接，理想交流电压表V接在电阻两端．整个空间有磁感应强度大小为B、方向竖直向下的匀强磁场，导体棒ab在外力F作用下以角速度ω绕两圆环的中心轴OO′匀速转动，产生正弦交流电．已知重力加速度为g.求：

(1) 导体棒ab沿环运动过程中受到的安培力最大值Fm；

(2) 电压表的示数U和导体棒从环的最低点运动到与环心等高处过程中通过电阻R的电荷量q；

(3) 导体棒ab从环的最低点运动半周到最高点的过程中外力F做的功W.

【题目】为了探究力对初速度为零的物体做功与物体获得速度的关系，某实验小组采用如图（甲）所示的装置进行实验。

(1)实验小组按正确的操作，将木板一端倾斜来平衡摩擦力，打出如上三条纸带，其中符合实验要求的是（选填纸带的字母编号）_______。

(2)下列关于橡皮筋及其做功的说法正确的是__________ 。

A．橡皮筋做功的值不需要测量

B．增加规格相同的橡皮筋条数，使橡皮筋对小车做的功成整数倍增加

C．在小车运动的过程中，橡皮筋一直对其做功

D．将橡皮筋的长度拉伸为原来的两倍，橡皮筋做的功增加了两倍

(3)在操作正确的前提下，其中打出的一条纸带如图（乙）所示，为了测量小车获得的速度，应选用纸带的部分进行测量；

(4)在某次实验中，实验小组误将木板水平放置，小车在橡皮筋作用下由静止开始运动，当小车运动到某一位置，橡皮筋恰好处于原长状态。下列说法正确的是______ 。

A．此时小车速度最大

B．此时小车加速度最大

C．此后小车开始做匀速直线运动

D．当小车速度最大时，橡皮筋一定处于拉伸状态

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网