题目内容
9.课外活动小组的同学设计了一个实验方案,用来测算缠绕螺线管的金属丝长度.已知缠绕螺线管的金属丝电阻较小,经查阅资料得知该金属丝的电阻率为ρ.(1)实验中用螺旋测微器测得金属丝的直径,如图甲所示,可知金属丝的直径为d=1.125mm.
(2)若测得的金属丝直径用d表示,电阻用R表示,则由已知量和测得量的符号表示金属丝的长度L=$\frac{π{d}^{2}R}{4ρ}$.
(3)小组的同学用多用电表进行了几次测量,指针分别处于a、b位置,如图乙所示,若多用电表的选择开关处于下面表格中所指的档位,a和b的相应读数是多少?请填在表格中
| 指针位置 | 选择开关 所处档位 | 读 数 |
| a | 直流电流100mA | 23.0mA |
| 直流电压2.5V | 0.57V | |
| b | 电阻×100 | 350Ω |

分析 (1)螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数.
(2)应用电阻定律可以求出金属丝的长度.
(3)多用电表的使用中,能测量电流、直流电压、交流电压、电阻等.有关表头读数:最上示数是电阻刻度;中间是直、交流电压或电流刻度;最下示数是交流量程是2.5V电压刻度.因此当选择开关位于电阻档时,先读出刻度盘上的读数,然后再乘上倍率就是电阻的阻值.注意的是电阻刻度是不均匀的,所以尽量让指针指在中间附近.当选择开关位于电压档时,根据电压量程从而选择刻度读数.同样电流档也是一样的.只有当小于2.5V的交流电压时,才读最下方刻度.
解答 解:(1)由图甲所示螺旋测微器可知,固定刻度示数为1mm,可动刻度示数为12.5×0.01mm=0.125mm,螺旋测微器示数为1mm+0.125mm=1.125mm.
(2)由电阻定律可知,金属丝电阻R=ρ$\frac{L}{S}$=ρ$\frac{L}{π(\frac{d}{2})^{2}}$,
则金属丝长度L=$\frac{π{d}^{2}R}{4ρ}$.
(3)直流电流100mA档读第二行“0~10”一排,最小度值为2mA估读到1mA就可以,故读数为:23.0mA;
直流电压2.5V档读第二行“0~250”一排,最小分度值为0.05V估读到0.01V就可以,故读数为:0.57V;
电阻×100档读第三行,测量值等于表盘上读数“3.5”乘以倍率“100”. 故读数为:350Ω
故答案如下表所示:
| 指针位置 | 选择开关 所处档位 | 读 数 |
| a | 直流电流100mA | 23.0mA |
| 直流电压2.5V | 0.57V | |
| b | 电阻×100 | 350Ω |
(3)23.0,0.57±0.01,350;
点评 螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数,螺旋测微器需要估读;应用电阻定律即可求出电阻率的表达式;
让学生熟悉如何使用多用电表,并知道多用电表能测哪里物理量.同时知道电阻刻度盘是不均匀的,除刻度盘上的读数外还要乘上倍率;还有量程2.5V的交流电压是读最下面刻度.

 用三根轻绳将质量为m的物块悬挂在空中,如图所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )
用三根轻绳将质量为m的物块悬挂在空中,如图所示.已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )| A. | $\frac{\sqrt{3}}{2}$mg $\frac{1}{2}$mg | B. | $\frac{1}{2}$mg $\frac{\sqrt{3}}{2}$mg | C. | $\frac{\sqrt{3}}{4}$mg $\frac{1}{2}$mg | D. | $\frac{1}{2}$mg $\frac{\sqrt{3}}{4}$mg |
 如图所示,平行板电容器的两极板A、B接在电池的两极,一带正电的小球悬挂在电容器内部,闭合开关S,给电容器充电,稳定后悬线偏离竖直方向的夹角为θ,则( )
如图所示,平行板电容器的两极板A、B接在电池的两极,一带正电的小球悬挂在电容器内部,闭合开关S,给电容器充电,稳定后悬线偏离竖直方向的夹角为θ,则( )| A. | 若保持开关S闭合,A极板向B极板靠近,则θ增大 | |
| B. | 若保持开关S闭合,A极板向B极板靠近,则θ不变 | |
| C. | 若开关S断开,A极板向B极板靠近,则θ不变 | |
| D. | 若开关S断开,A极板向B极板靠近,则θ增大 |
 风洞是对飞机、导弹性能进行检测的一种高科技产物,现代汽车的生产也有
风洞是对飞机、导弹性能进行检测的一种高科技产物,现代汽车的生产也有运用风洞技术进行检测的,如图所示是小丽所在兴趣小组设计的一个类似于风洞的实验装置,他们在桌面上放有许多大小不同的塑料球,这些塑料球的密度均为ρ,用水平向左恒定的风作用在球上,使它们做匀加速运动(摩擦不计).
已知风对球的作用力F与球的最大横截面积S成正比,即F=kS,k为一常量.对塑料球来说,可以认为空间存在一个风力场,在该风力场中风力对球做功与路径无关.( )
| A. | 可以定义风力场强度E=$\frac{F}{S}$=k,方向与风力相同 | |
| B. | 风力场强度E与塑料球受到的风力成正比 | |
| C. | 若以栅栏P为风力势能参考平面,距P为x处的风力势能是Ep=kx | |
| D. | 以栅栏P为风力势能参考平面,塑料小球的半径用r表示,某时刻的速度用v表示,风力场中机械能守恒定律可写为kπr2x+$\frac{2}{3}$ρπr3v2=恒量 |
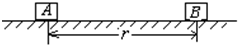 如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:
如图所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求: 如图为A、B两个电阻的电压-电流图象,根据图象可得到:RA=10Ω,RB=20Ω;若将两个电阻分别接入电路时,两电阻两端电压之比为16:5,则通过它们的电流之比为32:5.
如图为A、B两个电阻的电压-电流图象,根据图象可得到:RA=10Ω,RB=20Ω;若将两个电阻分别接入电路时,两电阻两端电压之比为16:5,则通过它们的电流之比为32:5. 如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C 带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取π=3.
如图所示,在xOy坐标系中,x轴上N点到O点的距离是12cm,虚线NP与x轴负向的夹角是30°.第Ⅰ象限内NP的上方有匀强磁场,磁感应强度B=1T,第IV象限有匀强电场,方向沿y轴正向.一质量m=8×10-10kg.电荷量q=1×10-4C 带正电粒子,从电场中M(12,-8)点由静止释放,经电场加速后从N点进入磁场,又从y轴上P点穿出磁场.不计粒子重力,取π=3.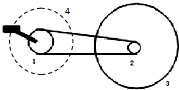 如图所示是自行车传动机构的示意图,其中1是大齿轮,2是小齿轮,3是后车轮,4是脚踏板.已知脚踏板的转速为n(r/s),要知道自行车前进的速度有多大,除需要测量大齿轮1的半径r1和小齿轮2的半径r2外,还需要测量的物理量及符号是后轮的半径R,请用上述物理量的符号推导出自行车前进速度的表达式为$\frac{{2πnRr}_{1}}{{r}_{2}}$.
如图所示是自行车传动机构的示意图,其中1是大齿轮,2是小齿轮,3是后车轮,4是脚踏板.已知脚踏板的转速为n(r/s),要知道自行车前进的速度有多大,除需要测量大齿轮1的半径r1和小齿轮2的半径r2外,还需要测量的物理量及符号是后轮的半径R,请用上述物理量的符号推导出自行车前进速度的表达式为$\frac{{2πnRr}_{1}}{{r}_{2}}$.