题目内容
如图所示,两根不计电阻的金属导线MN与PQ放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行,M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。金属棒处于位置(I)时,给金属棒一个向右的速度v1=4 m/s,同时方向水平向右的外力F1 ="3" N作用在金属棒上使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,大小变为F2,金属棒向右做匀速直线运动,经过时间t ="2" s到达位置(Ⅲ)。金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m,金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点。已知s1="7.5" m。求:(1)金属棒向右匀减速运动时的加速度大小?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?

(1)金属棒从位置(I)到位置(Ⅱ)的过程中,加速度不变,方向向左,设大小为a,在位置I时,a、b间的感应电动势为E1,感应电流为I1,受到的安培力为F安1,则
E1=BL1 v1,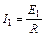 ,F安1
,F安1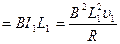 ···································①
···································①
F安1="4" N·································································②
根据牛顿第二定律得
F安1-F1 =ma·····························································③
a=" 1" m / s2·································································④
(2)设金属棒在位置(Ⅱ)时速度为v2,由运动学规律得
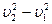 =-2a s1···························································⑤
=-2a s1···························································⑤
v2=" 1" m / s·································································⑥
由于在(I)和(II)之间做匀减速直线运动,即加速度大小保持不变,外力F1恒定,所以AB棒受到的安培力不变即F安1=F安2
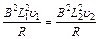 ···························································⑦
···························································⑦
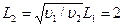 m······················································⑧
m······················································⑧
(3)金属棒从位置(Ⅱ)到位置(Ⅲ)的过程中,做匀速直线运动,感应电动势大小与位置(Ⅱ)时的感应电动势大小相等,安培力与位置(Ⅱ)时的安培力大小相等,所以
F2= F安2="4" N······························································⑨
(4) 设位置(II)和(Ⅲ)之间的距离为s2,则
s2= v2t="2" m ································································⑩
设从位置(I)到位置(Ⅱ)的过程中,外力做功为W1,从位置(Ⅱ)到位置(Ⅲ)的过程中,外力做功为W2,则
W1= F1 s1="22.5" J ···························································11
W2= F2 s2="8" J······························································12
根据能量守恒得W1+ W2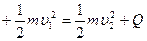 ·······························13·
·······························13·
解得Q =" 38" J ·····························································14


E1=BL1 v1,
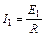 ,F安1
,F安1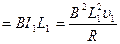 ···································①
···································①F安1="4" N·································································②
根据牛顿第二定律得
F安1-F1 =ma·····························································③
a=" 1" m / s2·································································④
(2)设金属棒在位置(Ⅱ)时速度为v2,由运动学规律得
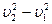 =-2a s1···························································⑤
=-2a s1···························································⑤v2=" 1" m / s·································································⑥
由于在(I)和(II)之间做匀减速直线运动,即加速度大小保持不变,外力F1恒定,所以AB棒受到的安培力不变即F安1=F安2
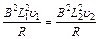 ···························································⑦
···························································⑦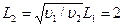 m······················································⑧
m······················································⑧(3)金属棒从位置(Ⅱ)到位置(Ⅲ)的过程中,做匀速直线运动,感应电动势大小与位置(Ⅱ)时的感应电动势大小相等,安培力与位置(Ⅱ)时的安培力大小相等,所以
F2= F安2="4" N······························································⑨
(4) 设位置(II)和(Ⅲ)之间的距离为s2,则
s2= v2t="2" m ································································⑩
设从位置(I)到位置(Ⅱ)的过程中,外力做功为W1,从位置(Ⅱ)到位置(Ⅲ)的过程中,外力做功为W2,则
W1= F1 s1="22.5" J ···························································11
W2= F2 s2="8" J······························································12
根据能量守恒得W1+ W2
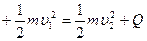 ·······························13·
·······························13·解得Q =" 38" J ·····························································14



略

练习册系列答案
相关题目






 的金属杆CD,金属杆与轨道接触良好,整个回路电阻为R,倾斜轨道与水平面夹角为
的金属杆CD,金属杆与轨道接触良好,整个回路电阻为R,倾斜轨道与水平面夹角为 。有一一个与水平轨道平面垂直、方向向下、磁感应强度为B1的匀强磁场;有另一个与倾斜轨道平面垂直、磁感应强度为B2的匀强磁场。为了使CD能够静止,金属杆船在外力F作用下向左匀速运动,试问:
。有一一个与水平轨道平面垂直、方向向下、磁感应强度为B1的匀强磁场;有另一个与倾斜轨道平面垂直、磁感应强度为B2的匀强磁场。为了使CD能够静止,金属杆船在外力F作用下向左匀速运动,试问:
 ( )
( ) 转动
转动