题目内容
 如图所示,在光滑绝缘水平面两端有两块平行带电金属板A、B,其间存在着场强E=200N/C的匀强电场,靠近正极板B处有一薄挡板S.一个带电小球,质量为m=1×10-2kg、电量q=-2×10-3C,开始时静止在P点,它与挡板S的距离为h=5cm,与A板距离为H=45cm.静止释放后小球在电场力的作用下向左运动,与挡板S相碰后电量减少到碰前的K倍,K=5/6,碰撞前后小球的速度大小不变.
如图所示,在光滑绝缘水平面两端有两块平行带电金属板A、B,其间存在着场强E=200N/C的匀强电场,靠近正极板B处有一薄挡板S.一个带电小球,质量为m=1×10-2kg、电量q=-2×10-3C,开始时静止在P点,它与挡板S的距离为h=5cm,与A板距离为H=45cm.静止释放后小球在电场力的作用下向左运动,与挡板S相碰后电量减少到碰前的K倍,K=5/6,碰撞前后小球的速度大小不变.(1)设匀强电场中挡板S所在位置的电势为零,则电场中P点的电势Up为多少?小球在P点时的电势能?p为多少
(2)小球第一次与挡板S碰撞时的速度多大?第一次碰撞后小球能运动到离A板多远的地方?
分析:(1)根据电势差与电场强度的关系求出SP之间的电势差,进而求出P点的电势Up,电势能EP=qUp.
(2)根据动能定理求出小球第一次到达挡板S时的速度;设小球与挡板相碰后向右运动s,根据动能定理即可求解;
(2)根据动能定理求出小球第一次到达挡板S时的速度;设小球与挡板相碰后向右运动s,根据动能定理即可求解;
解答:解:(1)由题意,S所在位置的电势为零,则P点的电势Up为Up=-Eh=-200×5×10-2V=-10V
小球在P点时的电势能ε=q?UP=-2×103×(-10)J=0.02J
(2)小球向左运动的过程电场力做功:qEh=
mv2
∴v=
=2m/s
小球向右运动的过程电场力做功:-kqEh1=0-
mv2
解得,h1=0.06m
小球能运动到离A板的距离:x=h+H-h1=(0.45+0.05-0.06)m=0.44m
答:
(1)则电场中P点的电势为-10V,小球在P点时的电势能为0.02J;
(2)小球第一次与挡板S碰撞时的速度是2m/s,第一次碰撞后小球能运动到离A板0.44m的地方.
小球在P点时的电势能ε=q?UP=-2×103×(-10)J=0.02J
(2)小球向左运动的过程电场力做功:qEh=
| 1 |
| 2 |
∴v=
|
小球向右运动的过程电场力做功:-kqEh1=0-
| 1 |
| 2 |
解得,h1=0.06m
小球能运动到离A板的距离:x=h+H-h1=(0.45+0.05-0.06)m=0.44m
答:
(1)则电场中P点的电势为-10V,小球在P点时的电势能为0.02J;
(2)小球第一次与挡板S碰撞时的速度是2m/s,第一次碰撞后小球能运动到离A板0.44m的地方.
点评:本题主要考查了带电粒子在电场中运动的问题,要知道电场力做的功等于电势差乘以电荷量,匀强电场中电场力做的功等于电场力乘以位移,注意动能定理在粒子运动的应用,难度适中.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
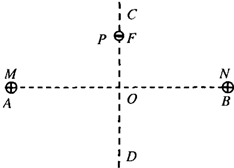 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )| A、小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小,则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中振幅不断减小 |
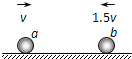 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( )
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( ) (2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
(2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为 如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,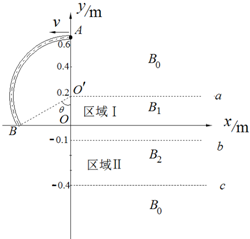 如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求:
如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求: