题目内容
 如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求:
如图所示,在光滑绝缘水平面上有直角坐标系xoy,将半径为R=0.4m,内径很小、内壁光滑、管壁极薄的圆弧形绝缘管AB水平固定在第二象限内,它的A端和圆心O′都在y轴上,B端在x轴上,O′B与y轴负方向夹角θ=60°.在坐标系的第一、四象限不同区域内存在着四个垂直于水平面的匀强磁场,a、b、c为磁场的理想分界线,它们的直线方程分别为a:y=0.2;b:y=-0.1;c:y=-0.4;在a、b所围的区域Ⅰ和b、c所围的区域Ⅱ内的磁感应强度分别为B1、B2,第一、四象限其它区域内磁感应强度均为B0.当一质量m=1.2×10-5kg、电荷量q=1.0×10-6C,直径略小于绝缘管内径的带正电小球,自绝缘管A端以v=2.0×10-2 m/s的速度垂直y轴射入管中,在以后的运动过程中,小球能垂直通过c、a,并又能以垂直于y轴的速度进入绝缘管而做周期性运动.求:(1)B0的大小和方向;
(2)B1、B2的大小和方向;.
(3)在运动的一个周期内,小球在经过第一、四 象限的过程中,在区域Ⅰ、Ⅱ内运动的时间与在区域Ⅰ、Ⅱ外运动的时间之比.
分析:(1)粒子在第一象限内做圆周运动,则由牛顿第二定律可求得磁感应强度,由左手定则可知磁场的方向;
(2)由题意可知,要使粒子能垂直ca且能周期性运动,则区域IⅠ、Ⅱ内小球运动的半径应相等,区域Ⅰ、Ⅱ的磁感应强度应等大反向,由几何关系可得出粒子的半径,由牛顿第二定律可求得磁感应强度;
(3)粒子在运动中速度大小不变,则由s=vt可求得各段中所需要的时间,即可求出比值.
(2)由题意可知,要使粒子能垂直ca且能周期性运动,则区域IⅠ、Ⅱ内小球运动的半径应相等,区域Ⅰ、Ⅱ的磁感应强度应等大反向,由几何关系可得出粒子的半径,由牛顿第二定律可求得磁感应强度;
(3)粒子在运动中速度大小不变,则由s=vt可求得各段中所需要的时间,即可求出比值.
解答: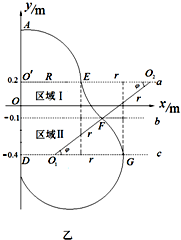
 解:(1)小球在第一象限过a做半径为R的匀速圆周运动
解:(1)小球在第一象限过a做半径为R的匀速圆周运动
由牛顿第二定律有:qB0v=m
解得:B0=
①
代入数据得:B0=0.6T
由左手定则知B0方向垂直水平面向下.
(2)要使小球不停的做周期性运动,则区域Ⅰ、Ⅱ内小球运动的半径应相等,区域Ⅰ、Ⅱ的磁感应强度应等大反向,B2的方向为垂直水平面向下,B1的方向为垂直水平面向上
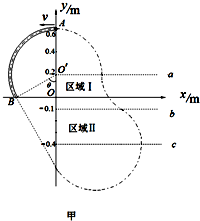
小球做周期性运动的径迹如图甲.
设在区域Ⅱ、Ⅰ内小球的圆心为O1、O2,小球圆周运动的半径为r,偏转角为φ,如图乙所示.
由几何知识知:2rsinφ=O′D②
R+r-DG=2rcosφ-r③
DG=(1+
)R④
解②③④得r=
R⑤
φ=
r=
⑥
解④⑤得 B1=0.4
T≈0.693T
则有:B2=B1=0.4
T≈0.693T
(3)由v=
知:
小球在第4象限过c以前做匀速圆周运动时间为t1=
⑦
小球在区域Ⅰ、区域Ⅱ做匀速圆周运动时间共为t2=
⑧
小球在第1象限区域Ⅰ以上做匀速圆周运动时间为 t3=
⑨
设在运动的一个周期内,小球在通过第一、四象限的过程中,在区域Ⅰ、Ⅱ内运动的时间与在区域Ⅰ、Ⅱ外时间之比为k则 k=
⑩
解⑤⑥⑦⑧⑨⑩得k=
.

 解:(1)小球在第一象限过a做半径为R的匀速圆周运动
解:(1)小球在第一象限过a做半径为R的匀速圆周运动由牛顿第二定律有:qB0v=m
| v2 |
| R |
解得:B0=
| mv |
| qR |
代入数据得:B0=0.6T
由左手定则知B0方向垂直水平面向下.
(2)要使小球不停的做周期性运动,则区域Ⅰ、Ⅱ内小球运动的半径应相等,区域Ⅰ、Ⅱ的磁感应强度应等大反向,B2的方向为垂直水平面向下,B1的方向为垂直水平面向上
小球做周期性运动的径迹如图甲.
设在区域Ⅱ、Ⅰ内小球的圆心为O1、O2,小球圆周运动的半径为r,偏转角为φ,如图乙所示.
由几何知识知:2rsinφ=O′D②
R+r-DG=2rcosφ-r③
DG=(1+
| ||
| 2 |
解②③④得r=
| ||
| 2 |
φ=
| π |
| 3 |
| mv |
| qB1 |
解④⑤得 B1=0.4
| 3 |
则有:B2=B1=0.4
| 3 |
(3)由v=
| s |
| t |
小球在第4象限过c以前做匀速圆周运动时间为t1=
| 5πR |
| 6v |
小球在区域Ⅰ、区域Ⅱ做匀速圆周运动时间共为t2=
| 2πr |
| 3v |
小球在第1象限区域Ⅰ以上做匀速圆周运动时间为 t3=
| πR |
| 2v |
设在运动的一个周期内,小球在通过第一、四象限的过程中,在区域Ⅰ、Ⅱ内运动的时间与在区域Ⅰ、Ⅱ外时间之比为k则 k=
| t2 |
| t1+t3 |
解⑤⑥⑦⑧⑨⑩得k=
| ||
| 4 |
点评:本题为高考压轴题,难度较大,要求学生能有较好的想象力,在解答此题时一定要注意通过画图去找出题目中所给出的条件所说明的情景,从而根据所学的半径公式及周期公式进行求解.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
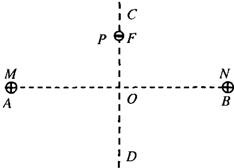 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )| A、小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小,则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中振幅不断减小 |
 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( )
如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动.某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰.则下列叙述正确的是( ) (2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
(2012?汕头一模)如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为 如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,