��Ŀ����
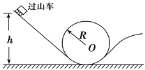
����Ŀ����ͼ��ʾ����һ����m=1kg��С��飬��ƽ̨���Գ��ٶ�v0=3m/sˮƽ�׳�������C��ʱ��ǡ����C������߷������̶���ˮƽ�����ϵİ뾶R=0.5m�Ĵֲ�Բ����������С��黬�Ͻ������ĩ��D�������ΪM=3kg�ij�ľ�壬ľ���ϱ�����Բ�����ĩ��������ƽ��ľ���±�����ˮƽ����֮��⻬�Ӵ�����С�����ľ�������ľ���˶�l=1mʱ����ľ���й�ͬ�ٶȣ�С����볤ľ��֮��Ķ�Ħ��������=0.3��C���Բ����Բ����������ֱ����ļн���=53�������ƿ���������ȡg=10m/s2��sin53��=0.8��cos53��=0.6����
(1)A��C����ĸ߶Ȳ�h��
(2)����Ҫ����Բ�����ĩ��D��ʱ�Թ����ѹ����
(3)���ͨ��Բ������˷�Ħ�������Ĺ���

���𰸡�(1)0.8m�� (2) 26N��������ֱ���£�(3) 10.5J
��������
(1).С��鵽C��ʱ���ٶ���ֱ����Ϊ
vCy=v0tan53�� =4 m/s
����ĸ߶�
![]()
(2).С�����ľ���ϻ��дﵽ��ͬ�ٶȵĹ��̣�ľ��ļ��ٶȴ�С��
a1=��mg /M =0.3��10/3=1m/s2
���ļ��ٶȴ�С��
a2=��mg /m =��g=3m/s2
������ã�
![]()
![]()
�������ϸ�ʽ���������ݽ��
![]()
С����D��ʱ
![]()
�������ݽ��
FN=26N
��ţ�ٵ������ɵ�
FN��=FN=26 N
������ֱ����
(3).С�����A��D�Ĺ����У���˷�Ħ�������Ĺ�ΪWf ���ɶ��ܶ����У�
![]()
�������ݽ��
Wf =10.5J