题目内容
11. 如图所示,长度为l的绝缘细线将质量为m、电量为q的带正电小球悬挂于O点,整个空间 中充满了匀强电场.(取sin37°=0.6,cos37°=0.8)
如图所示,长度为l的绝缘细线将质量为m、电量为q的带正电小球悬挂于O点,整个空间 中充满了匀强电场.(取sin37°=0.6,cos37°=0.8)(1)当电场方向竖直向上时,若使小球在A点获得水平速度v1=$\sqrt{2gl}$,小球刚好能在竖直平面内做完整的圆周运动,求电场强度E1;
(2)当电场方向水平,且电场强度E2=$\frac{4mg}{3q}$时,要不能让细线松弛,求小球在A点获得的水平速度v2应该满足的条件.
分析 (1)当电场方向竖直向上时,小球所受的电场力竖直向上,若电场力小于重力,小球到达最高点时速度最小.若小球刚好能通过最高点,由电场力和重力的合力充当向心力,由牛顿第二定律求最小速度,再由动能定理求出电场强度.若电场力大于重力,小球通过最低点时速度最小.若小球刚好能通过最低点,由电场力和重力的合力充当向心力,由牛顿第二定律求电场强度.
(2)让细线不松弛有两种可能的情况:一种小球能做完整的圆周运动,另一种来回摆动.第一种情况,找到等效“最高点”,即电场力和重力的合力指向圆心的位置,求出等效“最高点”的速度,由动能定理求得水平速度v2.再由动能定理求出小球来回摆动时水平速度v2,即可得到水平速度v2应满足的条件.
解答 解:(1)当电场力qE1<mg时,小球在最高点的速度v最小,若小球刚好能通过最高点,
则在最高点有:mg-qE1=m$\frac{{v}^{2}}{l}$
从最低点到最高点,由动能定理得:-(mg-qE1)•2l=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{1}^{2}$
解得 E1=$\frac{3mg}{5q}$
当电场力qE1>mg时,小球在最低点的速度v最小,若小球刚好能通过最低点,则在最低点有:qE1-mg=m$\frac{{v}^{2}}{l}$
解得 E1=$\frac{3mg}{q}$
联立可得要使小球做完整的圆周运动,电场强度应满足:$\frac{3mg}{5q}$≤E1≤$\frac{3mg}{q}$.
(2)当电场方向水平,且E2=$\frac{4mg}{3q}$时,小球所受重力为mg、电场力qE2的合力大小为
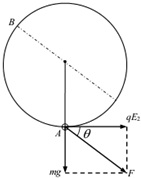
F=$\sqrt{(mg)^{2}+(q{E}_{2})^{2}}$=$\frac{5}{3}$mg,与水平方向的夹角θ满足tanθ=$\frac{mg}{q{E}_{2}}$=$\frac{3}{4}$
如果小球获得水平速度v2后刚好能做完整的圆周运动,在速度最小的位置B(如图)满足
F=m$\frac{{v}_{B}^{2}}{l}$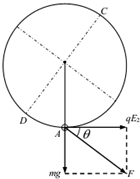
小球从A点运动到B点,由动能定理得:
-mgl(1+sinθ)-qE2lcosθ=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{2}^{2}$
联立解得 v2=$\sqrt{7gl}$
如果小球获得水平速度v2后来回摆动,则小球刚好能到达C点或D点(如上图),则小球从A点运动到C点,由动能定理得:
-mgl(1+cosθ)+qE2lsinθ=0-$\frac{1}{2}m{v}_{2}^{2}$
或小球从A点运动到D点,由动能定理得:
-mgl(1-cosθ)-qE2lsinθ=0-$\frac{1}{2}m{v}_{2}^{2}$
解得 v2=$\sqrt{2gl}$
综合可得,v2≥$\sqrt{7gl}$或v2≤$\sqrt{2gl}$细线均不会松驰
答:(1)小球刚好能在竖直平面内做完整的圆周运动,电场强度E1应满足$\frac{3mg}{5q}$≤E1≤$\frac{3mg}{q}$.
(2)当电场方向水平,且电场强度E2=$\frac{4mg}{3q}$时,要不能让细线松弛,小球在A点获得的水平速度v2应该满足的条件是v2≥$\sqrt{7gl}$或v2≤$\sqrt{2gl}$.
点评 解决本题的关键要找到物理的最高点,即速度最小的位置,分析小球通过此位置的临界条件,运用牛顿运动定律和动能定理结合研究这类临界问题.


| A. | 0~6s内物体做匀变速直线运动 | |
| B. | 2~4s内物体做匀变速直线运动 | |
| C. | 3s末物体的速度为零,且改变运动方向 | |
| D. | 2s末物体的速度大小为4m/s |
| A. | t1=t2 | B. | t1>t2 | ||
| C. | t1<t2 | D. | 以上说法都有可能 |
| A. | 5m,5m | B. | 5m,3m | C. | 4m,3m | D. | 4m,1m |
| A. | 0.5A | B. | 0.6A | C. | 0.8A | D. | 1A |
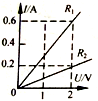 电阻R1、R2的伏安特性曲线如图所示,则电阻R1:R2=1:3.若把R1、R2并联后接到电源上时,R1消耗的电功率是6W,电阻R2消耗的功率为2W.
电阻R1、R2的伏安特性曲线如图所示,则电阻R1:R2=1:3.若把R1、R2并联后接到电源上时,R1消耗的电功率是6W,电阻R2消耗的功率为2W. 电梯上升运动的v-t图如图所示,从图象可知:
电梯上升运动的v-t图如图所示,从图象可知: