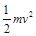题目内容
 在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:(1)两滑块碰撞后刚结合在一起的共同速度v;
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s.
分析:(1)设两滑块碰前A的速度为v1,由动能定理求出v1,A、B两滑块碰撞过程动量守恒,根据动量守恒定律即可求解;
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理即可求得弹簧压缩量,弹簧压缩过程中电场力做正功,电势能的减少量等于电场力所做的功;设反弹后A、B滑行了x2距离后速度减为零,由动能定理求得x2,比较电场力与滑动摩擦力的关系,判断滑块的运动情况,最终求出最大距离.
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理即可求得弹簧压缩量,弹簧压缩过程中电场力做正功,电势能的减少量等于电场力所做的功;设反弹后A、B滑行了x2距离后速度减为零,由动能定理求得x2,比较电场力与滑动摩擦力的关系,判断滑块的运动情况,最终求出最大距离.
解答:解:(1)设两滑块碰前A的速度为v1,
由动能定理有:qEl-μmgl=
m
解得:v1=3m/s
A、B两滑块碰撞,由于时间极短动量守恒,
设共同速度为vmv1=(M+m)v
解得:v=1.0m/s
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,
由动能定理有:qEx1-μ(M+m)gx1-E0=0-
(M+m)v2
解得:x1=0.02m
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:E0-qEx2-μ(M+m)gx2=0
解得:x2≈0.05m
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离
为:S=x2+s-x1=0.05m+0.05m-0.02m=0.08m
答:(1)两滑块碰撞后刚结合在一起的共同速度v为1m/s.
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s为0.08m.
由动能定理有:qEl-μmgl=
| 1 |
| 2 |
| v | 2 1 |
解得:v1=3m/s
A、B两滑块碰撞,由于时间极短动量守恒,
设共同速度为vmv1=(M+m)v
解得:v=1.0m/s
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,
由动能定理有:qEx1-μ(M+m)gx1-E0=0-
| 1 |
| 2 |
解得:x1=0.02m
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:E0-qEx2-μ(M+m)gx2=0
解得:x2≈0.05m
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离
为:S=x2+s-x1=0.05m+0.05m-0.02m=0.08m
答:(1)两滑块碰撞后刚结合在一起的共同速度v为1m/s.
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s为0.08m.
点评:本题主要考查了动能定理和动量守恒定律的直接应用,要培养自己分析物理过程,解决综合题的能力.

练习册系列答案
相关题目
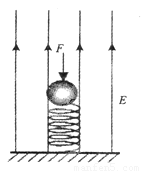
如图,竖直向上的匀强电场中,绝缘轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球,小球与弹簧不连接,施加外力F将小球向下压至某位置静止。现撤去F,使小球沿竖直方向运动,在小球由静止到离开弹簧的过程中,重力、电场力对小球所做的功分别为W1和W2,小球离开弹簧时的速度为v,不计空气阻力,则上述过程中( )
| A.小球的重力势能增加-W1 | B.小球的电势能减少W2 |
C.小球的机械能增加W1+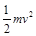 | D.小球与弹簧组成的系统机械能守恒 |
 如图所示,绝缘的轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球(小球与弹簧不拴接),整个系统处在方向竖直向上的匀强电场中.开始时,整个系统处于静止状态,现施加一外力F,将小球向下压至某一位置,然后撤去外力,使小球从静止开始向上运动.设小球从静止开始向上运动到离开弹簧的过程中,电场力对小球所做的功为W1,小球克服重力所做的功为W2,小球离开弹簧时的速度为V.不计空气阻力,则在上述过程中( )
如图所示,绝缘的轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球(小球与弹簧不拴接),整个系统处在方向竖直向上的匀强电场中.开始时,整个系统处于静止状态,现施加一外力F,将小球向下压至某一位置,然后撤去外力,使小球从静止开始向上运动.设小球从静止开始向上运动到离开弹簧的过程中,电场力对小球所做的功为W1,小球克服重力所做的功为W2,小球离开弹簧时的速度为V.不计空气阻力,则在上述过程中( ) (1)如图所示,一轻质弹簧竖直立在水平地面上,弹簧一端固定在地面上.一小球从高处自由下落到弹簧上端,将弹簧压缩至最低点.在小球开始下落至最低点的过程中,弹簧始终处于弹性限度内.在此过程中,能正确表示小球的加速度a随下降位移x的大小变化关系是下面图象中的
(1)如图所示,一轻质弹簧竖直立在水平地面上,弹簧一端固定在地面上.一小球从高处自由下落到弹簧上端,将弹簧压缩至最低点.在小球开始下落至最低点的过程中,弹簧始终处于弹性限度内.在此过程中,能正确表示小球的加速度a随下降位移x的大小变化关系是下面图象中的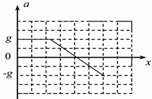 B.
B.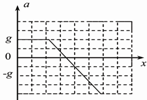 C.
C.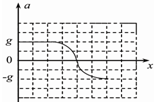 D.
D.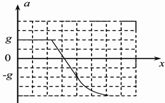
 电动势为E,电源的内阻忽略不计,信号放大器、信号转换器和显示器的分流作用忽略不计.求:
电动势为E,电源的内阻忽略不计,信号放大器、信号转换器和显示器的分流作用忽略不计.求: 如图所示,竖直向上的匀强电场中,绝缘轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球,小球与弹簧不连接,施加外力F将小球向下压至某位置静止.现撤去F,使小球沿竖直方向运动,在小球由静止到离开弹簧的过程中,重力、电场力对小球所做的功分别为W1和W2,小球离开弹簧时的速度为v,不计空气阻力,则该过程中( )
如图所示,竖直向上的匀强电场中,绝缘轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球,小球与弹簧不连接,施加外力F将小球向下压至某位置静止.现撤去F,使小球沿竖直方向运动,在小球由静止到离开弹簧的过程中,重力、电场力对小球所做的功分别为W1和W2,小球离开弹簧时的速度为v,不计空气阻力,则该过程中( )