题目内容
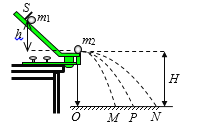
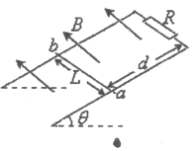
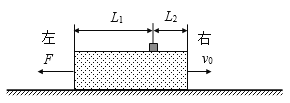
【题目】如图，上表面光滑、下表面粗糙的木板放置于水平地面上，可视为质点的滑块静止放在木板的上表面。t = 0时刻，给木板一个水平向右的初速度v0，同时对木板施加一个水平向左的恒力F，经一段时间，滑块从木板上掉下来。已知木板质量M =3 kg，高h = 0.2 m，与地面间的动摩擦因数=0.2；滑块质量m =0.5 kg，初始位置距木板左端L1=0.46 m，距木板右端L2=0.14 m；初速度v0=2 m/s，恒力F = 8 N，重力加速度g=10 m/s2。求：
（1）滑块从离开木板开始到落至地面所用时间；
（2）滑块离开木板时，木板的速度大小；
（3）从t = 0时刻开始到滑块落到地面的过程中，摩擦力对木板做的功。
【答案】1）0.2s（2）0.6m/s（3）-7.38J
【解析】试题分析：由于A上表面光滑，小物块B与木板A间无摩擦则小物块B离开木板A前始终对地静止，滑块离开后做自由落体运动，由
来计算时间；由于A上表面光滑则小物块B离开木板A前始终对地静止，木板A在恒力和摩擦力共同作用下先向右匀减速后向左匀加速，对木板应用牛顿第二定律求出加速度，根据运动学公式即可求解时间；摩擦力做功为
，s为木板运动的路程．
（1）设滑块从离开木板开始到落到地面所用时间为t0，以地面为参考系，滑块离开木板后做自由落体运动，根据运动学公式知
，得
（2）以木板为研究对象，向右做匀减速直线运动，由牛顿第二定律
得a1=5m/s2，则木板减速到零所经历的时间
所经过的位移
由于s1＜L1=0.46m，表明这时滑块仍然停留在木板上
此后木板开始向左做匀加速直线运动，摩擦力的方向改变，由牛顿第二定律
得a2=
m/s2
滑块离开木板时，木板向左的位移
该过程根据运动学公式
，得t2=1.8s
滑块滑离瞬间木板的速度
（3）滑块离开木板后，木板所受地面的支持力及摩擦力随之改变，由牛顿第二定律
得a3=
m/s2
故木板在
这段时间的位移为
整个过程摩擦力对木板做的功为
得
