题目内容
15. 如图所示,A、B两球均看成质点,B球静止于光滑的水平面上,与竖直墙壁相距为x,A球以某一初速度向B球运动并发生第一次碰撞,已知两球的第二次碰撞发生在距离竖直墙壁为$\frac{1}{2}$x处,若题中的所有碰撞都没有能量损失,求:
如图所示,A、B两球均看成质点,B球静止于光滑的水平面上,与竖直墙壁相距为x,A球以某一初速度向B球运动并发生第一次碰撞,已知两球的第二次碰撞发生在距离竖直墙壁为$\frac{1}{2}$x处,若题中的所有碰撞都没有能量损失,求:①A、B两球的质量之比
②两球的第三次碰撞发生在何处?
分析 ①两求出碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械守恒定律可以求出两球的质量之比.
②两求出碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械守恒定律与两球的路程关系可以求出第三次碰撞的位置.
解答 解:①A、B碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mAv0=mAv1+mBv2,
由机械能守恒定律的:$\frac{1}{2}$mAv02=$\frac{1}{2}$mAv12+$\frac{1}{2}$mBv22,
两球第二次碰撞发生在$\frac{1}{2}$x处,则B的路程为A的路程的3倍,
它们的运动时间t相等,则它们的速度关系为:v2=3v1,
解得:$\frac{{m}_{A}}{{m}_{B}}$=$\frac{3}{1}$;
②以向右为正方向,B球与墙壁碰撞后以等大的速度反弹,对于第二次碰撞,由动量守恒定律得:
mAv1-mBv2=mAv1′+mBv2′,
由机械性能守恒定律的:$\frac{1}{2}$mAv12+$\frac{1}{2}$mBv22=$\frac{1}{2}$mAv1′2+$\frac{1}{2}$mBv2′2,
解得:v1′=-$\frac{{v}_{0}}{2}$,v2′=$\frac{3{v}_{0}}{2}$ (v1′=$\frac{{v}_{0}}{2}$,v2′=-$\frac{3{v}_{0}}{2}$ 不符合题意,舍去)
A向左运动,B向右运动,B与墙壁碰撞反弹后向左运动,然后与A发生第三次碰撞,则A、B发生第三次碰撞时:$\frac{x+{x}_{A}}{x}$=$\frac{3}{1}$,
解得:xA=$\frac{1}{2}$x,
A在第二次碰撞后向左运动的路程为$\frac{1}{2}$x的路程与B发生第三次碰撞,
两球发生第三次碰撞在墙壁左边的x处.
答:①A、B两球的质量之比为3:1;
②两球的第三次碰撞发生在墙壁左边距离为x处.
点评 本题考查了求小球的质量之比、碰撞发生的位置,两球碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以解题,小球与墙壁碰撞时无机械能损失,碰撞后反向弹回,弹回的速度大小不变.

 长度为1m的轻杆OA,A端有一质量为2kg的小球,以O点为圆心,在竖直平面内做圆周运动,如图所示,小球通过最高点时的速度为3m/s,取g=10m/s2,则此时小球将( )
长度为1m的轻杆OA,A端有一质量为2kg的小球,以O点为圆心,在竖直平面内做圆周运动,如图所示,小球通过最高点时的速度为3m/s,取g=10m/s2,则此时小球将( )| A. | 受到2N的拉力 | B. | 受到18N的拉力 | C. | 受到2N的支持力 | D. | 受到38N的支持力 |
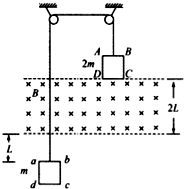 (多选题)如图所示,正方形导线框ABCD、abcd的边长均为L,电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,且正方形导线框与定滑轮处于同一竖直平面内.在两导线框之间有一宽度为2L、磁感应强度大小为B、方向垂直纸面向里的匀强磁场.开始时导线框ABCD的下边与匀强磁场的上边界重合,导线框abcd的上边到匀强磁场的下边界的距离为L.现将系统由静止释放,当导线框ABCD刚好全部进入磁场时,开始做匀速运动.不计摩擦和空气阻力,则( )
(多选题)如图所示,正方形导线框ABCD、abcd的边长均为L,电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,且正方形导线框与定滑轮处于同一竖直平面内.在两导线框之间有一宽度为2L、磁感应强度大小为B、方向垂直纸面向里的匀强磁场.开始时导线框ABCD的下边与匀强磁场的上边界重合,导线框abcd的上边到匀强磁场的下边界的距离为L.现将系统由静止释放,当导线框ABCD刚好全部进入磁场时,开始做匀速运动.不计摩擦和空气阻力,则( )| A. | 匀速运动的速度大小v=$\frac{mgR}{{{B^2}{L^2}}}$ | |
| B. | 两线框刚开始做匀速运动时轻绳上的张力FT=mg | |
| C. | 导线框abcd通过磁场的时间t=$\frac{{2{B^2}{L^3}}}{mgR}$ | |
| D. | 两线框从开始运动至等高的过程中所产生的总焦耳热Q=2mgL-$\frac{{3{m^3}{g^2}{R^2}}}{{2{B^4}{L^4}}}$ |
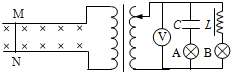 如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t在导轨上左右来回运动,两灯A、B都发光.下列说法中正确的是( )
如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t在导轨上左右来回运动,两灯A、B都发光.下列说法中正确的是( )| A. | 只增大T,则灯A变暗、灯B变亮 | |
| B. | 当时间t=T时,电压表的示数为零 | |
| C. | 只将副线圈上的滑动触头下滑时,两灯均变暗,电压表的示数变小 | |
| D. | 只增大v0,两灯都变亮 |
| A. | $\sqrt{2}$:4 | B. | 2$\sqrt{2}$:1 | C. | 1:4 | D. | 1:8 |
| A. | 布朗远动就是液体分子的无规则运动 | |
| B. | 布朗运动是液体分子无规则运动的反映 | |
| C. | 布朗运动就是组成布朗微粒的固体分子的无规则运动 | |
| D. | 布朗运动是组成布朗微粒的固体分子无规则运动的反映 |
 如图所示,甲、乙两个交流电路中,两电源的输出电压和输出电流均相等,已知甲乙电路中两电阻的比值为4:1,则乙电路中理想变压器的原副线圈匝数比为4:1.
如图所示,甲、乙两个交流电路中,两电源的输出电压和输出电流均相等,已知甲乙电路中两电阻的比值为4:1,则乙电路中理想变压器的原副线圈匝数比为4:1.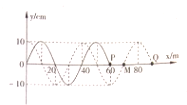 沿x轴传播的机械波在零时刻的波形如图中实线所示,虚线为波在0.15s时刻波形图,此时Q点开始振动,据图中的信息,求:
沿x轴传播的机械波在零时刻的波形如图中实线所示,虚线为波在0.15s时刻波形图,此时Q点开始振动,据图中的信息,求: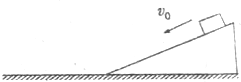 如图所示,用同种材料制成的倾角为37°的斜面和长水平面,斜面长11.25m且固定,一小物块从斜面顶端以初速度v0沿斜面下滑,如果v0=3.6m/s,则经过3.0s后小物块停在斜面上,不考虑小物块到达斜面底端时因碰撞损失的能量,求:(sin37°=0.6,cos37°=0.8)
如图所示,用同种材料制成的倾角为37°的斜面和长水平面,斜面长11.25m且固定,一小物块从斜面顶端以初速度v0沿斜面下滑,如果v0=3.6m/s,则经过3.0s后小物块停在斜面上,不考虑小物块到达斜面底端时因碰撞损失的能量,求:(sin37°=0.6,cos37°=0.8)