题目内容
质量为m、带电荷量为q的粒子（忽略重力）在磁感应强度为B的匀强磁场中做匀速圆周运动，形成空间环形电流．已知粒子的运动速率为v、半径为R、周期为T，环形电流的大小为I．则下面说法正确的是（ ）
分析：本题是洛伦兹力充当向心力的一个综合应用．
由洛伦兹力充当向心力的速度公式可以判定A；
由洛伦兹力充当向心力的角速度公式即线速度与角速度关系可以判定B；
由洛伦兹力充当向心力的周期公式可以求出周期，然后再求电流，可以判定C；
由C的解答可以判定D．
由洛伦兹力充当向心力的速度公式可以判定A；
由洛伦兹力充当向心力的角速度公式即线速度与角速度关系可以判定B；
由洛伦兹力充当向心力的周期公式可以求出周期，然后再求电流，可以判定C；
由C的解答可以判定D．
解答：解：
A：由洛伦兹力充当向心力得：qvB=m
，解得
=
，故A错误．
B：由洛伦兹力充当向心力得：qvB=mRω2，又v=Rω，代入得：qRωB=mRω2，解得：ω=
，故t时间内转过的圆心角为：θ=ωt=
，故B正确．
C：由洛伦兹力充当向心力得：qvB=mR
，又：v=
，代入得：q
B=mR
，化简得到：qB=m
，解得：T=
，由电流定义式得环形电流：I=
=
，与速度无关，故电流大小不变，故C正确．
D：由洛伦兹力充当向心力得：qvB=mR
，又：v=
，代入得：q
B=mR
，化简得到：qB=m
，解得：T=
，即周期与速度无关，故D错误．
故选：BC
A：由洛伦兹力充当向心力得：qvB=m
| v2 |
| R |
| q |
| m |
| v |
| RB |
B：由洛伦兹力充当向心力得：qvB=mRω2，又v=Rω，代入得：qRωB=mRω2，解得：ω=
| qB |
| m |
| qBt |
| m |
C：由洛伦兹力充当向心力得：qvB=mR
| 4π2 |
| T2 |
| 2πR |
| T |
| 2πR |
| T |
| 4π2 |
| T2 |
| 2π |
| T |
| 2πm |
| qB |
| q |
| T |
| q2B |
| 2πm |
D：由洛伦兹力充当向心力得：qvB=mR
| 4π2 |
| T2 |
| 2πR |
| T |
| 2πR |
| T |
| 4π2 |
| T2 |
| 2π |
| T |
| 2πm |
| qB |
故选：BC
点评：本题需要熟练掌握磁场圆周运动中，洛伦兹力充当向心力的各种表达式，由此可以判定各个选项，其次需要留意我们不常用得到的一些知识，如圆心角的求法这里用的是角速度定义的变形式，另有的时候还可以用其定义来求圆心角．
练习册系列答案
相关题目
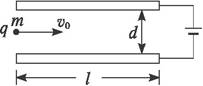
如图所示，质量为m、带电荷量为+q的粒子，从两平行电极板正中央垂直电场线和磁感线以速度v飞入．已知两极间距为d，磁感应强度为B，这时粒子恰能沿直线穿过电场和磁场区域．今将磁感应强度增大到某值，则粒子将落到极板上．已知粒子重力不计，则粒子落到极板上时的动能为多少？
如图所示，有一质量为m，带电荷量为+q的小球（可视为质点），自竖直向下、场强为E的匀强电场中的P点静止下落．在P点正下方距离h处有一弹性绝缘挡板S（挡板不影响匀强电场的分布），小球每次与挡板S相碰后电荷量均减少到碰前的k倍（k＜1），而碰撞过程中小球的机械能不损失．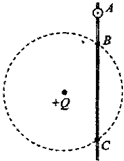
如图所示：光滑绝缘杆竖直放置，它与以正电荷Q为圆心的某一圆周交于B、C两点，质量为m，带电荷量为+q的有孔小球从杆上A点无初速下滑，已知q＜Q，AB=h，小球滑到B点的速度大小为
