��Ŀ����
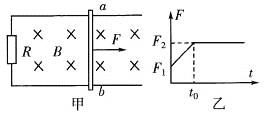
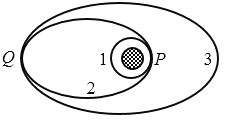
����Ŀ��ij��������С������ͼ���е�װ��̽��������ٶ�������������֮��Ĺ�ϵ��ͼ�У���������̨�̶�һ���ʻ��֣�ͨ��������ֵ�����ϸ��������ͬ���������A��B��������ΪM�����A����ճ��С�ڹ�Ƭ�������Ϊd���������Բ��ơ������A��B�¸���5����ͬ��С���룬������Ϊm��0.010kg�������C��Dͨ�����˹̶�������̨�ϣ�������ͬһ��ֱ���ϣ��ҹ����C��D֮��ľ���Ϊh��������������ּ�ʱ��������ͼ��δ�������ɼ�¼�ڹ�Ƭͨ������ŵ�ʱ�䡣����װ���ִ��ھ�ֹ״̬��ȡ���ص��������ٶ�g��9.8m/s2��ʵ�鲽�����£�
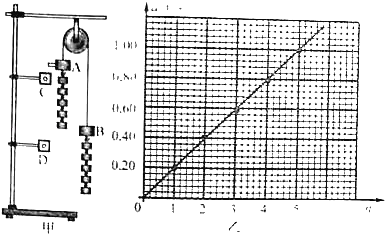
��1����n������ȡn��1��2��3��4��5������������B���¶�ժ�²��������A�¶˵Ĺ������档�ͷ���飬�ü�ʱ����¼�ڹ�Ƭͨ�������C��D��ʱ��t1��t2�����ȱ����˶����ɿɵõ����A������̵ļ��ٶ�a��_____���á�h��d��t1��t2����ʾ��
��2����С��ͬѧ���������ݼ��±������ǽ������е�����ת��Ϊ����㻭��ͼ�ҵ�����ϵ�У�������a��nͼ��ͼ����Եó�������������һ��ʱ������ļ��ٶ��������ܵ�������_____�������ȡ����ȡ�����
N | a/s��2 |
1 | 0.20 |
2 | 0.41 |
3 | 0.59 |
4 | 0.79 |
5 | 1.00 |
��3����С��ͬѧ����a��nͼ��һ��������A����B��������MΪ_____kg������2λ��Ч���֣���
��4����ʵ�������Ħ��������Ӱ�����ԣ��ɿ��ɶ�ֵ���������������õ����������M�IJ���ֵ_____���������ֱʵֵ������ڡ�����С�ڡ����ڡ���
���𰸡�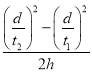 �� ���ȣ� 0.44�� ����
�� ���ȣ� 0.44�� ����
��������
(1)���Aͨ�������C��Dʱ���ٶȣ�![]() ����C��D���̣����ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�ã�
����C��D���̣����ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�ã�![]() �����ٶȣ�
�����ٶȣ�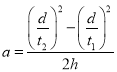 ��
��
(2)��A��B�������10��С������ɵ�ϵͳΪ�о�����
��ţ�ٵڶ����ɵã�2nmg����10m+2M��a����ͼʾͼ���֪������ļ��ٶ��������ܵ����������ȡ�
(3)��ţ�ٵڶ����ɵã�![]() ����ͼʾa��nͼ���֪��ͼ���б�ʣ�
����ͼʾa��nͼ���֪��ͼ���б�ʣ�
![]() ����ã�M��0.44kg��
����ã�M��0.44kg��
(4)��������f����ţ�ٵڶ����ɵã�2nmg��f����10m+2M��a�����ٶȣ�![]() ��ͼ���б�ʲ�������f��Ӱ�죬���Զ��������M�IJ���ֵ���䡣
��ͼ���б�ʲ�������f��Ӱ�죬���Զ��������M�IJ���ֵ���䡣

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�