题目内容
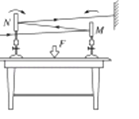
【题目】如图，ABD为竖直平面内的光滑绝缘轨道，其中AB段是水平的，BD段为半径R=0.2m的半圆，两段轨道相切于B点，整个轨道处在竖直向下的匀强电场中，场强大小E=5.0×103V/m。一不带电的绝缘小球甲，以速度
沿水平轨道向右运动，与静止在B点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为m=1.0×10-2kg，乙所带电荷量q=2.0×10-5C，g取10m/s2。(水平轨道足够长，甲、乙两球可视为质点，整个运动过程无电荷转移)
（1） 甲乙两球碰撞后，乙恰能通过轨道的最高点D，求乙在轨道上的首次落点到B点的距离；
（2）在满足(1)的条件下。求的甲的速度；
（3）若甲仍以速度向右运动，增大甲的质量，保持乙的质量不变，求乙在轨道上的首次落点到B点的距离范围。
【答案】（1）0.4m；（2）2
m/s；（3）0.4m≤x'＜1.6m。
【解析】
（1）在乙恰能通过轨道的最高点的情况下，设乙到达最高点的速度为vD，乙离开D点到达水平轨道的时间为t，乙的落点到B点的距离为x，
则由向心力公式得 
①
竖直方向匀加速运动 
水平方向匀速运动 x=vDt
联立得：x=0.4m
（2）设碰撞后甲、乙的速度分别为v甲、v乙，根据动量守恒有：
mv0=mv甲+mv乙
根据机械能守恒定律有：
联立得：v甲=0，v乙=v0
由动能定理得：
联立得：
（3）设甲的质量为M，碰撞后甲、乙的速度分别为vM、vm，根据动量守恒有：
Mv0=MvM+mvm
根据机械能守恒定律有
有以上两式可得：
由于Mm，可得：v0≤vm＜2v0
设乙球过D点的速度为vD′，
由动能定理得
联立以上两个方程可得：2m/s≤vD′＜8m/s
设乙在水平轨道上的落点到B点的距离为x'，则有：x'=vD′t
所以可以解得：0.4m≤x'＜1.6m
名校课堂系列答案
【题目】某物理课外小组利用图甲中的装置探究物体加速度与其所受外力之间的关系。图中，利用铁架台固定一轻质滑轮，通过跨过滑轮的轻质细绳悬吊相同的两个物块A、B，质量均为M，物块A侧面粘贴小遮光片，其宽度为d、质量忽略不计。在物块A、B下各挂5个相同的小钩码，质量均为m＝0.010kg。光电门C、D通过连杆固定于铁架台上，并处于同一竖直线上，且光电门C、D之间的距离为h。两光电门与数字计时器相连（图中未画出）可记录遮光片通过光电门的时间。整个装置现处于静止状态，取当地的重力加速度g＝9.8m/s2．实验步骤如下：
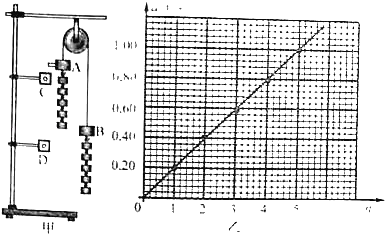
（1）将n（依次取n＝1，2，3，4，5）个钩码从物块B的下端摘下并挂在物块A下端的钩码下面。释放物块，用计时器记录遮光片通过光电门C、D的时间t1、t2．由匀变速运动规律可得到物块A下落过程的加速度a＝_____（用“h、d、t1、t2”表示）
（2）该小组同学测量的数据见下表。他们将表格中的数据转变为坐标点画在图乙的坐标系中，并作出a﹣n图象。从图象可以得出：当物体质量一定时，物体的加速度与其所受的外力成_____（“正比”或“反比“）。
N | a/s﹣2 |
1 | 0.20 |
2 | 0.41 |
3 | 0.59 |
4 | 0.79 |
5 | 1.00 |
（3）该小组同学利用a﹣n图象，进一步求得物块A（或B）的质量M为_____kg（保留2位有效数字）。
（4）若实验过程中摩擦阻力的影响明显（可看成定值），用上述方法得到的物块质量M的测量值_____物块质量的直实值（填“大于”，“小于”或“等于”）
