题目内容
粗糙水平面上AB两点间距s=75m，一质量m=10kg的物体受到水平方向成37°的斜向上的力F=100N作用，物体由静止开始
经5s从A运动到B．
（1）求物体与水平面间的动摩擦因数；
（2）如果仅要求使物体从A运动到B，力F并不需要一直作用，求使物体能从A运动到B，力F做功的最小值．（cos37°=0.8，sin37°=0.6，g=10m/s2）
经5s从A运动到B．（1）求物体与水平面间的动摩擦因数；
（2）如果仅要求使物体从A运动到B，力F并不需要一直作用，求使物体能从A运动到B，力F做功的最小值．（cos37°=0.8，sin37°=0.6，g=10m/s2）
分析：（1）根据位移的关系可以求得加速度的大小，再根据物体的受力的情况可以求得摩擦因数的大小；
（2）从A到B的过程中，物体先加速再减速运动到B，根据加速运动的位移可以求得拉力做功的大小．
（2）从A到B的过程中，物体先加速再减速运动到B，根据加速运动的位移可以求得拉力做功的大小．
解答：解：（1）由运动学公式有s=
at2，
解得：a=
=6m/s2，
对物体由牛顿运动定律有：
Fcos37°-f=ma
N=mg-Fsin37°
f=μN
代入数据解得：μ=
=0.5
（2）设力F最小作用距离为s1，撤去力F后物体具有速度为v，再运动距离为s2，刚好运动到B停止．
则有：s1=
，s2=
，s1+s2=s
其中：a′=
=μg=5m/s2，为撤去F时物体的加速度．
代入数据解得：s1=
s=
m
则此时力F做功最小值为：W=Fs1cos37°=
J=2727.3J．
答：（1）物体与水平面间的动摩擦因数为0.5；
（2）力F做功的最小值为2727.3J．
| 1 |
| 2 |
解得：a=
| 2s |
| t2 |
对物体由牛顿运动定律有：
Fcos37°-f=ma
N=mg-Fsin37°
f=μN
代入数据解得：μ=
| Fcos37°-ma |
| mg-Fsin37° |
（2）设力F最小作用距离为s1，撤去力F后物体具有速度为v，再运动距离为s2，刚好运动到B停止．
则有：s1=
| v2 |
| 2a |
| v2 |
| 2a′ |
其中：a′=
| μmg |
| m |
代入数据解得：s1=
| 5 |
| 11 |
| 375 |
| 11 |
则此时力F做功最小值为：W=Fs1cos37°=
| 30000 |
| 11 |
答：（1）物体与水平面间的动摩擦因数为0.5；
（2）力F做功的最小值为2727.3J．
点评：本题是度牛顿第二定律的应用，对物体受力分析是解本题的关键，在计算功的大小的时候要注意拉力并不是在整个过程中都对物体有拉力的作用．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
（2010?如皋市模拟）如图所示，粗糙的绝缘水平面上，A、B两点相距4L，O为AB的中点，且AC=CO=OD=DB，A、B两处分别固定有电量为+Q的点电荷．在C点处有一个质量为优的小物块（可视为质点），带电量为+q（q《Q），以初速度才．向右滑行，通过O点后恰好在D点处停下并保持静止，求：
（2011?龙岩模拟）如图，AB为一光滑固定轨道，AC为摩擦因素μ=0.25的粗糙水平轨道，D为水平地面上的一点，且B、C、D在同一竖直线上，已知B、C两点的高度差为h，C、D两点的高度差也为h，AC两点相距s=2h．两滑块从A点以相同的初速度v0分别沿两轨道滑行，到达B点或C点后分别水平抛出，欲使两滑块的落地点相同，滑块的初速度v0应满足什么条件？
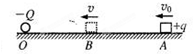如图所示，O、B、A为一粗糙绝缘水平面上的三个点，三个点在同一条直线上，一电荷量为-Q的点电荷固定在O点，现有一质量为m，电荷量为+q的小金属块（可视为质点），从A点以初速度υ0沿它们的连线向固定点电荷运动，到B点时速度最小，其大小为υ（υ＜υ0）．已知小金属块与水平面间的动摩擦因数为μ，AB间距离为L，静电引力常数为k，则（ ）