题目内容
 (2011?龙岩模拟)如图,AB为一光滑固定轨道,AC为摩擦因素μ=0.25的粗糙水平轨道,D为水平地面上的一点,且B、C、D在同一竖直线上,已知B、C两点的高度差为h,C、D两点的高度差也为h,AC两点相距s=2h.两滑块从A点以相同的初速度v0分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度v0应满足什么条件?
(2011?龙岩模拟)如图,AB为一光滑固定轨道,AC为摩擦因素μ=0.25的粗糙水平轨道,D为水平地面上的一点,且B、C、D在同一竖直线上,已知B、C两点的高度差为h,C、D两点的高度差也为h,AC两点相距s=2h.两滑块从A点以相同的初速度v0分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度v0应满足什么条件?分析:滑块1沿光滑曲面滑行,只有重力做功,机械能守恒,求出B点速度后,再根据平抛运动的位移公式求出射程x1;对于滑块2,先根据动能定理求出C点速度,再根据平抛运动的分位移公式求解出射程x2,根据两个滑块水平分位移相等列式求解出A点的初速度.
解答:解:对与滑块1,从A到B过程机械能守恒,有
m
=
m
+mgh
得 vB=
从B点抛出后,有
x1=vBt
2h=
gt2
解得
x1=2
?
对于滑块2,从A到C过程,由动能定理,得到
-μmgS=
m
-
m
由于μ=0.5,根据几何关系S=2h,得vc=
=
从C点抛出后:
得x2=
?
依题意有:x1=x2
解得:v0=
即滑块的初速度v0应满足v0=
.
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 B |
得 vB=
|
从B点抛出后,有
x1=vBt
2h=
| 1 |
| 2 |
解得
x1=2
|
|
对于滑块2,从A到C过程,由动能定理,得到
-μmgS=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 0 |
由于μ=0.5,根据几何关系S=2h,得vc=
|
|
从C点抛出后:
|
得x2=
|
|
依题意有:x1=x2
解得:v0=
| 3gh |
即滑块的初速度v0应满足v0=
| 3gh |
点评:本题关键是分析清楚两个滑块的运动情况,然后对滑块的各个运动过程运用相应的规律列式求解.

练习册系列答案
相关题目

 (2011?龙岩模拟)如图所示,公共汽车沿水平面向右做匀变速直线运动,小球A用细线悬挂车顶上,质量为m的一位中学生手握扶杆始终相对于汽车静止地站在车箱底板上.学生鞋底与公共汽车间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻公共汽车对学生产生的作用力的大小和方向为( )
(2011?龙岩模拟)如图所示,公共汽车沿水平面向右做匀变速直线运动,小球A用细线悬挂车顶上,质量为m的一位中学生手握扶杆始终相对于汽车静止地站在车箱底板上.学生鞋底与公共汽车间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻公共汽车对学生产生的作用力的大小和方向为( )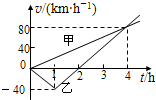 (2011?龙岩模拟)甲、乙两汽车在平直公路上从同一地点同时开始行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
(2011?龙岩模拟)甲、乙两汽车在平直公路上从同一地点同时开始行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( ) (2011?龙岩模拟)如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )
(2011?龙岩模拟)如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )