题目内容
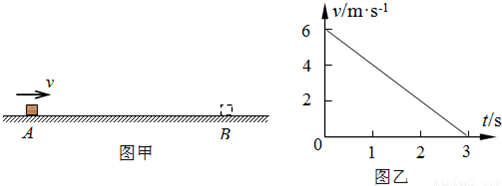
如图甲所示,一个小滑块以一定的初速度从粗糙的水平面上的A点运动至B点停止,在该过程中滑块的速度-时间(v-t)图象如图乙所示.(取g=10m/s2)
求:
(1)AB两点间的距离s;
(2)滑块与水平面间的动摩擦因素μ.

求:
(1)AB两点间的距离s;
(2)滑块与水平面间的动摩擦因素μ.
分析:(1)速度图象与两坐标轴所围成的“面积”大小等于位移,由几何知识求出AB两点间的距离s;
(2)速度图象斜率的大小等于加速度,可求出加速度,由牛顿第二定律求解动摩擦因素μ.
(2)速度图象斜率的大小等于加速度,可求出加速度,由牛顿第二定律求解动摩擦因素μ.
解答:解:(1)速度图象与两坐标轴所围成的“面积”大小,即为AB两点间的距离,
故有s=
×6×3m=9m
(2)滑块运动的加速度大小等于图象斜率的大小,则有 a=
=
m/s2=2m/s2
根据牛顿第二定律得:f=μmg=ma
解得:μ=
=
=0.2
答:(1)AB两点间的距离s是9m;
(2)滑块与水平面间的动摩擦因素μ为0.2.
故有s=
| 1 |
| 2 |
(2)滑块运动的加速度大小等于图象斜率的大小,则有 a=
| △v |
| △t |
| 6 |
| 3 |
根据牛顿第二定律得:f=μmg=ma
解得:μ=
| a |
| g |
| 2 |
| 10 |
答:(1)AB两点间的距离s是9m;
(2)滑块与水平面间的动摩擦因素μ为0.2.
点评:本题首先要有读图能力,抓住速度图象与两坐标轴所围成的“面积”大小等于位移、斜率的大小等于加速度是关键.

练习册系列答案
相关题目
 将一长木板静止放在光滑的水平面上,如图甲所示,一个小铅块(可视为质点)以水平初速度v0由木板左端向右滑动,到达右端时恰能与木板保持相对静止.小铅块运动过程中所受的摩擦力始终不变,现将木板分成A和B两段,使B的长度和质量均为A的2倍,并紧挨着放在原水平面上,让小铅块仍以初速度v0由木块A的左端开始向右滑动,如图乙所示,则下列有关说法正确的是( )
将一长木板静止放在光滑的水平面上,如图甲所示,一个小铅块(可视为质点)以水平初速度v0由木板左端向右滑动,到达右端时恰能与木板保持相对静止.小铅块运动过程中所受的摩擦力始终不变,现将木板分成A和B两段,使B的长度和质量均为A的2倍,并紧挨着放在原水平面上,让小铅块仍以初速度v0由木块A的左端开始向右滑动,如图乙所示,则下列有关说法正确的是( )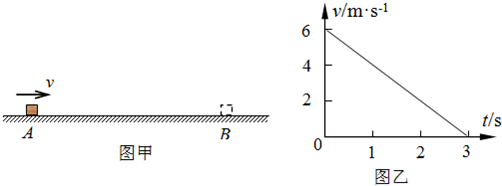
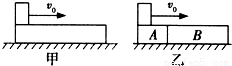 将一长木板静止放在光滑的水平面上,如图甲所示,一个小铅块(可视为质点)以水平初速度v由木板左端向右滑动,到达右端时恰能与木板保持相对静止.小铅块运动过程中所受的摩擦力始终不变,现将木板分成A和B两段,使B的长度和质量均为A的2倍,并紧挨着放在原水平面上,让小铅块仍以初速度v由木块A的左端开始向右滑动,如图乙所示,则下列有关说法正确的是( )
将一长木板静止放在光滑的水平面上,如图甲所示,一个小铅块(可视为质点)以水平初速度v由木板左端向右滑动,到达右端时恰能与木板保持相对静止.小铅块运动过程中所受的摩擦力始终不变,现将木板分成A和B两段,使B的长度和质量均为A的2倍,并紧挨着放在原水平面上,让小铅块仍以初速度v由木块A的左端开始向右滑动,如图乙所示,则下列有关说法正确的是( )