题目内容
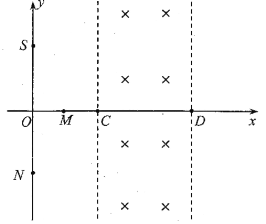
【题目】如图所示，xOy为一平面直角坐标系，O为坐标原点，S（0，L）、M（0.5L， 0）、N（0，-L）分别为坐标平面内的三个点，在x＜L的区域存在平行于xOy平面但方向未知的匀强电场，在L≤x≤2.5L的区域存在方向垂直xOy平面向里的匀强磁场。S点有一粒子源，能向平面内的任意方向发射质量为m、电荷量为+q、速率为v0的带电粒子。一粒子从S点射出后通过M点时速率为
；另一粒子从S点射出后通过N点时的速率为3v0。还有一粒子从S点沿x轴正方向射出，一段时间后该粒子从磁场左边界进入磁场，经磁场偏转后从磁场右边界射出磁场，该粒子在磁场中运动的时间为其在磁场中做匀速圆周运动周期的四分之一。不计粒子重力和粒子之间的相互作用，求：
（1）S、M间的电势差与S、N间的电势差；
（2）匀强电场的电场强度；
（3）匀强磁场的磁感应强度大小。
【答案】（1）USM=
，USN=
；（2）E=
，方向沿y轴负方向；（3）B=
【解析】
（1）粒子从S到M，据动能定理可得：
解得： 
粒子从S到N，据动能定理可得： 
则
（2）因
，可知OC为等势线，可得匀强电场方向沿y轴负方向
则
，方向沿y轴负方向
（3）从S点向x轴正方向射出的粒子，在电场和磁场中的运动轨迹图如图所示：
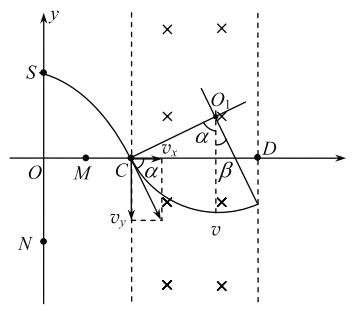
从S点向x轴正方向射出的粒子，在电场中做类平抛运动，到达磁场左边界，则：
，
，
以上式子联立解得：y=L
可知粒子从C点进入磁场，粒子通过C点时的速度与通过M点速度大小相等，可得粒子在C点处的速度大小及方向为：
，
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力：
据几何关系可得：
据题意：
解得：
练习册系列答案
相关题目
