题目内容
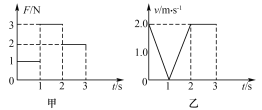
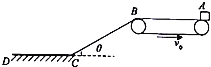
【题目】如图所示，长s=16m、倾斜角θ=370的斜面各通过一小段光滑圆弧与水平传送带和水平地面平滑连接，传送带长L=3．2m，以恒定速率v0=4m/s逆时针运行，将一质点物块轻轻地放上传送带右端A，物块滑到传送带左端B时恰好与传送带共速并沿斜面下滑，已知物块和传送带、斜面、水平地面间的动摩擦因数μ相同，物块最终静止在水平面上的D点，令物块在B、C处速率不变，取g=10m/s2，（sin37°=0．6，cos37°=0．8）求：
（1）动摩擦因数μ的值；
（2）物块滑到C点时的速度的大小；
（3）物块从A到D所经历的时间
【答案】（1）0.5 （2）1s （3）3s
【解析】
试题（1）物块在传送带上做匀加速直线运动，加速度：
，
由牛顿第二定律得：μmg=ma，
解得：μ=0．25；
（2）从B到C，由动能定理得：mgSsinθ-μmgScosθ=
mvC2-mv02
解得：vC=12m/s；
（3）在传送带上的加速度为a=2．5m/s2，到达传送带左端所需的时间为：
在水平面上运动的时间为
从A到D经历的时间：t=t1+t2+t3=8．4s
练习册系列答案
相关题目
