题目内容
 如图所示,长木板A长度为l,其右边固定一个薄挡板,包括挡板在内总质量为1.5M,静止在光滑的水平面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与挡板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A的左端停止,B与A之间的动摩擦因数为μ,求:
如图所示,长木板A长度为l,其右边固定一个薄挡板,包括挡板在内总质量为1.5M,静止在光滑的水平面上.小木块B质量为M,从A的左端开始以初速度v0在A上滑动,滑到右端与挡板发生碰撞,已知碰撞过程时间极短,碰后木块B恰好滑到A的左端停止,B与A之间的动摩擦因数为μ,求:(1)B滑到A左端时的速度
(2)若μ=
3
| ||
| 160gl |
(3)讨论A和B在整个运动过程中,是否有可能在某一段时间里运动方向是向左的,如果不可能,说明理由;如果可能,求出发生这种情况的条件.
分析:(1)B在A上滑动过程,系统所受的合外力为零,动量守恒.木块B恰好滑到A的左端停止,两者速度相等,根据动量守恒列式求此时B的速度.
(2)B与挡板碰撞后的过程,根据动量守恒和能量守恒列式求出两个物体的速度,再对A,根据动能定理列式,求摩擦力对木板A做的功.
(3)通过分析A的受力情况和运动情况,判断A能否向左运动.根据动量守恒和能量结合分析B能否向左运动.
(2)B与挡板碰撞后的过程,根据动量守恒和能量守恒列式求出两个物体的速度,再对A,根据动能定理列式,求摩擦力对木板A做的功.
(3)通过分析A的受力情况和运动情况,判断A能否向左运动.根据动量守恒和能量结合分析B能否向左运动.
解答:解:(1)取向右方向为正方向.
根据动量守恒定律得:Mv0=(M+1.5M)v ①
得B滑到A左端时的速度v=0.4v0.方向向右.
(2)设B与挡板碰撞后瞬间,A、B的速度分别为v1和v2.
根据系统的动量守恒和能量守恒得:
Mv0=Mv1+1.5Mv2 ②
M
=
M
+
×1.5M
+μMl ③
对A,由动能定理得:摩擦力对木板A做功W=
×1.5Mv2-
×1.5M
④
联立②③④得:v1=
v0(另一解v1=
v0,小于
v0舍去),W=-
M
.
(3)A在运动过程中不可能向左运动.因为在B未与A碰撞瓣,A受的摩擦力向右,做匀加速运动,碰撞后A所受的摩擦力向左,做匀减速运动,直到最后共同速度仍向右,所以A在运动过程中不可能向左运动.
B在碰撞后,有可能向左运动,即v2<0,结合①②得:v1>
代入③得 μ>
又根据能量守恒得:
M
-
(M+1.5M)v2≥2μMl
得到 μ<
故B运动方向是向左的条件是
<μ≤
.
答:(1)B滑到A左端时的速度为0.4v0
(2)摩擦力对木板A做功为-
M
.
(3)A在运动过程中不可能向左运动.B运动方向是向左的条件是
<μ≤
.
根据动量守恒定律得:Mv0=(M+1.5M)v ①
得B滑到A左端时的速度v=0.4v0.方向向右.
(2)设B与挡板碰撞后瞬间,A、B的速度分别为v1和v2.
根据系统的动量守恒和能量守恒得:
Mv0=Mv1+1.5Mv2 ②
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
对A,由动能定理得:摩擦力对木板A做功W=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 2 |
联立②③④得:v1=
| 1 |
| 2 |
| 3 |
| 10 |
| 2 |
| 5 |
| 27 |
| 400 |
| v | 2 0 |
(3)A在运动过程中不可能向左运动.因为在B未与A碰撞瓣,A受的摩擦力向右,做匀加速运动,碰撞后A所受的摩擦力向左,做匀减速运动,直到最后共同速度仍向右,所以A在运动过程中不可能向左运动.
B在碰撞后,有可能向左运动,即v2<0,结合①②得:v1>
| 2v0 |
| 3 |
代入③得 μ>
2
| ||
| 15gl |
又根据能量守恒得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
得到 μ<
3
| ||
| 20gl |
故B运动方向是向左的条件是
2
| ||
| 15gl |
3
| ||
| 20gl |
答:(1)B滑到A左端时的速度为0.4v0
(2)摩擦力对木板A做功为-
| 27 |
| 400 |
| v | 2 0 |
(3)A在运动过程中不可能向左运动.B运动方向是向左的条件是
2
| ||
| 15gl |
3
| ||
| 20gl |
点评:正确应用动量守恒和功能关系列方程是解决这类问题的关键,尤其是弄清相互作用过程中的功能关系.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
如图所示,长木板A的右端与桌面相齐,木板与桌面间的动摩擦因素为p,今用一水平恒力F将A推出桌面,在长板开始翻转之前,木板的加速度将会( )
![]()
|
A. 
![]() 逐渐增大
逐渐增大
B. 不变
C. 先减小后增大
 如图所示,长木板A上右端有一物块B,它们一起在光滑的水平面上向左做匀速运动,速度v0=2.0m/s.木板左侧有一个与木板A等高的固定物体C.已知长木板A的质量为mA=1.0kg,物块B的质量为mB=3.0kg,物块B与木板A间的动摩擦因数μ=0.5,取g=10m/s2.
如图所示,长木板A上右端有一物块B,它们一起在光滑的水平面上向左做匀速运动,速度v0=2.0m/s.木板左侧有一个与木板A等高的固定物体C.已知长木板A的质量为mA=1.0kg,物块B的质量为mB=3.0kg,物块B与木板A间的动摩擦因数μ=0.5,取g=10m/s2.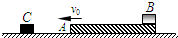 A:如图所示,长木板A上右端有一物块B,它们一起在光滑的水平面上向左做匀速运动,速度v0=2m/s.木板左侧有一个与木板A等高的固定物体C.已知长木板A的质量为mA=1.0kg,物块B的质量为mB=3.0kg,物块B与木板A间的动摩擦因数μ=0.5,取g=10m/s2.
A:如图所示,长木板A上右端有一物块B,它们一起在光滑的水平面上向左做匀速运动,速度v0=2m/s.木板左侧有一个与木板A等高的固定物体C.已知长木板A的质量为mA=1.0kg,物块B的质量为mB=3.0kg,物块B与木板A间的动摩擦因数μ=0.5,取g=10m/s2. (2007?湖南模拟)如图所示,长为L的木板A右边固定一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.另一质量为M的小木块B(视为质点),从木板A的左端开始以初速度为v0在木板A上滑动,小木块B与木板A间的动摩擦因数为μ,小木块B滑到木板A的右端与挡板发生碰撞,已知碰撞过程时间极短,且碰后木块B恰好滑到木板A的左端就停止滑动.求:
(2007?湖南模拟)如图所示,长为L的木板A右边固定一个挡板,包括挡板在内的总质量为1.5M,静止在光滑的水平地面上.另一质量为M的小木块B(视为质点),从木板A的左端开始以初速度为v0在木板A上滑动,小木块B与木板A间的动摩擦因数为μ,小木块B滑到木板A的右端与挡板发生碰撞,已知碰撞过程时间极短,且碰后木块B恰好滑到木板A的左端就停止滑动.求: =0.5,取g=10 m/s2。
=0.5,取g=10 m/s2。