题目内容
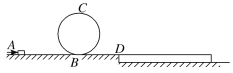
【题目】如图所示，ABCD是一个地面和轨道均光滑的过山车轨道模型，现对静止在A处的滑块施加一个水平向右的推力F，使它从A点开始做匀加速直线运动，当它水平滑行2.5 m时到达B点，此时撤去推力F、滑块滑入半径为0.5 m且内壁光滑的竖直固定圆轨道，并恰好通过最高点C，当滑块滑过水平BD部分后，又滑上静止在D处，且与ABD等高的长木板上，已知滑块与长木板的质量分别为0.2 kg、0.1 kg，滑块与长木板、长木板与水平地面间的动摩擦因数分别为0.3、
，它们之间的最大静摩擦力均等于各自滑动摩擦力，取g＝10 m/s2，求：
(1)水平推力F的大小；
(2)滑块到达D点的速度大小；
(3)木板至少为多长时，滑块才能不从木板上掉下来？在该情况下，木板在水平地面上最终滑行的总位移为多少？
【答案】（1）1N（2）
（3）t＝1 s ;
【解析】
(1)由于滑块恰好过C点，则有：
m1g＝m1
从A到C由动能定理得：
Fx－m1g·2R＝
m1vC2－0
代入数据联立解得：
F＝1 N
(2)从A到D由动能定理得：
Fx＝m1vD2
代入数据解得：
vD＝5 m/s
(3)滑块滑到木板上时，对滑块：
μ1m1g＝m1a1，
解得：
a1＝μ1g＝3 m/s2
对木板有：
μ1m1g－μ2(m1＋m2)g＝m2a2，
代入数据解得：
a2＝2 m/s2
滑块恰好不从木板上滑下，此时滑块滑到木板的右端时恰好与木板速度相同，
有：
v共＝vD－a1t
v共＝a2t，
代入数据解得：
t＝1 s
此时滑块的位移为：
x1＝vDt－a1t2，
木板的位移为：
x2＝a2t2，L＝x1－x2，
代入数据解得：
L＝2.5 m
v共＝2 m/s
x2＝1 m
达到共同速度后木板又滑行x′，则有：
v共2＝2μ2gx′，
代入数据解得：
x′＝1.5 m
木板在水平地面上最终滑行的总位移为：
x木＝x2＋x′＝2.5 m
