题目内容
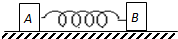 如图所示,静止在光滑水平面上的物体A和B质量分别为m和2m,它们之间用轻弹簧相连,在极短时间内对物体A作用一水平向右的冲量I,可知( )
如图所示,静止在光滑水平面上的物体A和B质量分别为m和2m,它们之间用轻弹簧相连,在极短时间内对物体A作用一水平向右的冲量I,可知( )分析:在极短时间内对物体A作用一水平向右的冲量I,说明A立即获得速度可由动量定理求出速度;通过动态分析可知当两者距离最小时速度相等,根据动量守恒定律可求出最小速度;再由能量守恒定律或机械能守恒定律求出弹性势能值.
解答:解;A、由动量定理知,由于作用时间极短,所以物体A立即获得速度,由I=△P=m
-0=m
,可得
=
,所以A正确.
B、A获得速度的瞬时物体A没有发生位移,弹簧没有发生压缩,故物体B仍静止,B错误.
C、A向右运动,弹簧逐渐压缩,A受到向左的弹力,物体B受到向右的弹力,向右做加速运动,由牛顿第二定律a=
可知,由a=
=
知,因x增大a随之增大,所以A做变减速运动,B做变加速运动,当两者速度相等时A、B距离最小,此时弹簧压缩到最短,由m
=(m+2m)v可得v=
=
,故C错误.
D、由上面分析知,当A与B之间距离最小时,A与B速度相等为v=
,再由能量守恒定律有
m
=
.(2m+m)
+
,解得
=
,故D正确.
故选AD.
| v | A |
| v | A |
| v | A |
| I |
| m |
B、A获得速度的瞬时物体A没有发生位移,弹簧没有发生压缩,故物体B仍静止,B错误.
C、A向右运动,弹簧逐渐压缩,A受到向左的弹力,物体B受到向右的弹力,向右做加速运动,由牛顿第二定律a=
| F |
| m |
| F |
| m |
| Kx |
| m |
| v | A |
| ||
| 3 |
| I |
| 3m |
D、由上面分析知,当A与B之间距离最小时,A与B速度相等为v=
| I |
| 3m |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 |
| E | P |
| E | P |
| ||
| 3m |
故选AD.
点评:注意一些关键词语如“极短时间内受到冲量”、“恰好”、“缓慢运动”等的含义;记住类似追击问题当两者相距为极值(最小值、最大值)时速度相等.

练习册系列答案
相关题目
 如图所示,静止在光滑水平面上的物体A,一端靠着处于自然状态的弹簧.现对物体作用一水平恒力,在弹簧被压缩到最短的过程中,物体的速度和加速度变化的情况是( )
如图所示,静止在光滑水平面上的物体A,一端靠着处于自然状态的弹簧.现对物体作用一水平恒力,在弹簧被压缩到最短的过程中,物体的速度和加速度变化的情况是( ) 如图所示,静止在光滑水平面上的小车质量为M=20kg.从水枪中喷的水柱,横截面积为S=10cm2,速度为v=10m/s,水的密度为ρ=1.0×103kg/m3.若用水枪喷出的水从车后沿水平方向冲击小车的前壁,且冲击到小车前壁的水全部沿前壁淌入小车中.
如图所示,静止在光滑水平面上的小车质量为M=20kg.从水枪中喷的水柱,横截面积为S=10cm2,速度为v=10m/s,水的密度为ρ=1.0×103kg/m3.若用水枪喷出的水从车后沿水平方向冲击小车的前壁,且冲击到小车前壁的水全部沿前壁淌入小车中. (2011?宜昌二模)如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,木板质量.M=3kg.质量m=1kg的铁块以水平速度v0=4m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中弹簧具有的最大弹性势能为( )
(2011?宜昌二模)如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,木板质量.M=3kg.质量m=1kg的铁块以水平速度v0=4m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中弹簧具有的最大弹性势能为( )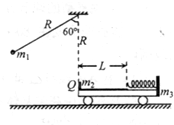 如图所示,静止在光滑水平面上的平板车,质量为m3=2kg,右端固定一自然伸长状态的轻弹簧,弹簧所在位置的车表面光滑,车左端和弹簧左端之间距离为L=0.75m,这部分车表面粗植,质量为m2=1kg的小物块Q,静止在平板车的左端.一不可伸长的轻质细绳长为R=2.5m,一端固定于Q正上方距Q为R处,另一端系一质量为m1=O.5kg的小球,将小球拉至悬线与竖直方向成60°角位置,由静止释放,小球到达最低点时与Q碰撞,时间极短,碰撞后小球反弹速度v0=lm/s,一段时间后Q恰好返回平板车左端静止.取g=10m/s2.求:
如图所示,静止在光滑水平面上的平板车,质量为m3=2kg,右端固定一自然伸长状态的轻弹簧,弹簧所在位置的车表面光滑,车左端和弹簧左端之间距离为L=0.75m,这部分车表面粗植,质量为m2=1kg的小物块Q,静止在平板车的左端.一不可伸长的轻质细绳长为R=2.5m,一端固定于Q正上方距Q为R处,另一端系一质量为m1=O.5kg的小球,将小球拉至悬线与竖直方向成60°角位置,由静止释放,小球到达最低点时与Q碰撞,时间极短,碰撞后小球反弹速度v0=lm/s,一段时间后Q恰好返回平板车左端静止.取g=10m/s2.求: (2008?福州模拟)如图所示,静止在光滑水平面的木板B的质量M=2.0kg.长度L=2.0m.铁块A静止于木板的右端,其质量m=1.0kg,与木板间的动摩擦因数μ=0.2,并可看作质点.现给木板B施加一个水平向右的恒定拉力F=8.0N,使木板从铁块下方抽出,试求:(取g=10m/s2)
(2008?福州模拟)如图所示,静止在光滑水平面的木板B的质量M=2.0kg.长度L=2.0m.铁块A静止于木板的右端,其质量m=1.0kg,与木板间的动摩擦因数μ=0.2,并可看作质点.现给木板B施加一个水平向右的恒定拉力F=8.0N,使木板从铁块下方抽出,试求:(取g=10m/s2)