题目内容
4.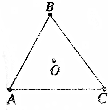 在绝缘的光滑水平桌面上,有三个带电小球A、B、C,带电量均为Q(正电),每个小球的质量均为m,各自位置分别位于边长为L的等边三角形的三个顶点,如图所示.假设本题中的带电小球均被视为点电荷,不计彼此间的万有引力作用.
在绝缘的光滑水平桌面上,有三个带电小球A、B、C,带电量均为Q(正电),每个小球的质量均为m,各自位置分别位于边长为L的等边三角形的三个顶点,如图所示.假设本题中的带电小球均被视为点电荷,不计彼此间的万有引力作用.(1)在三角形的中心O点应放置一个带何种带电性质、多少电量的带电小球,才能使四个小球都能静止?
(2)若中心电荷的带电量在(1)问基础上增加到原来的4倍,为了保持外围三个小球的相对位置不变,需让它们围绕中心电荷同时旋转起来,求它们旋转的线速度大小.
分析 (1)根据几何关系解出中心O点到三角形顶点的距离,每一个带电小球都处于静止状态,不妨研究A球,A球受力平衡,BC两球的对A是库仑斥力,O点的电荷2对A是库仑引力,列方程化简即可.
(2)若中心电荷带电荷量在(1)问基础上增加到原来的4倍,仍然研究A球,先求出A球受到的合力,再根据牛顿第二定律计算线速度.
解答 解:(1)由几何关系知:r=|AO|=$\frac{\frac{L}{2}}{cos30°}$L=$\frac{\sqrt{3}}{3}$L,A球受到BC两个正电荷的排斥力,合力的方向由O点指向A点;A受力平衡,则有:
F2=$\frac{kQq}{{r}^{2}}$=F1=2Fcos 30°
其中F=$\frac{k{Q}^{2}}{{L}^{2}}$,
所以q=$\frac{\sqrt{3}}{3}$Q,由F2的方向知q带负电.
(2)当q′=4q时,F2′=4F2
A球的合力F合=F2′-F1=4F2-F1=3F1=$\frac{3\sqrt{3}k{Q}^{2}}{{L}^{2}}$;
由牛顿第二定律:$\frac{3\sqrt{3}k{Q}^{2}}{{L}^{2}}$=$\frac{m{v}^{2}}{r}$.
代入数据联立得:v=$\sqrt{\frac{3k{Q}^{2}}{mL}}$
答:(1)在三角形的中心应放置负电荷,电荷量为$\frac{\sqrt{3}}{3}$Q.
(2)它们旋转的线速度大小为$\sqrt{\frac{3k{Q}^{2}}{mL}}$.
点评 本题关键是要能正确的选择研究对象,由于三个小球均处于静止状态,以其中一个球为研究对象根据平衡条件得出中心O点的电荷量,根据受力方向判断电荷的正负.

练习册系列答案
相关题目
14.做匀加速直线运动的列车出站时,车头经过站台某点O时速度是1m/s,车尾经过O点时的速度是7m/s,则这列列车的车身中点经过O点时的速度为( )
| A. | 4m/s | B. | 5m/s | C. | 6m/s | D. | 4.6m/s |
15. 物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
 物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )
物体从距地面高h处沿不同的支持面滑至地面,如图所示,a为光滑斜面,凸为粗糙斜面,c为粗糙曲面,物体的质量为m,在这三种过程中( )| A. | 重力做功相同 | B. | 沿c下滑时重力做功最大 | ||
| C. | 重力势能的变化相同 | D. | 沿c下滑时重力势能的变化量最大 |
12. 如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )
如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )
 如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )
如图所示,用细线将一小球悬挂在光滑墙壁上,小球的质量为m,若增加细线的长度,以下说法中正确的是( )| A. | 细线的拉力变大 | B. | 细线的拉力变小 | ||
| C. | 墙壁对球的支持力变小 | D. | 墙壁对球的支持力变大 |
19. 近日,在我国境内出现了观测条件最好的一次月全食.本次月全食阶段是月食过程中最为华美的一章,月全食期间的月亮变成了红铜色,如同一轮美丽的“红月亮”高挂在天空,持续时间有80分钟左右.下列说法正确的是( )
近日,在我国境内出现了观测条件最好的一次月全食.本次月全食阶段是月食过程中最为华美的一章,月全食期间的月亮变成了红铜色,如同一轮美丽的“红月亮”高挂在天空,持续时间有80分钟左右.下列说法正确的是( )
 近日,在我国境内出现了观测条件最好的一次月全食.本次月全食阶段是月食过程中最为华美的一章,月全食期间的月亮变成了红铜色,如同一轮美丽的“红月亮”高挂在天空,持续时间有80分钟左右.下列说法正确的是( )
近日,在我国境内出现了观测条件最好的一次月全食.本次月全食阶段是月食过程中最为华美的一章,月全食期间的月亮变成了红铜色,如同一轮美丽的“红月亮”高挂在天空,持续时间有80分钟左右.下列说法正确的是( )| A. | 17时14分指的是时间间隔 | |
| B. | 80分钟指的是时刻 | |
| C. | 在观测月全食时可将月亮看成质点 | |
| D. | 月亮绕地球做圆周运动,这是以地球为参考系来描述的 |
9.如图所示,闭合电路,当滑动变阻器滑动片P移动时,电流表示数的变化情况是( )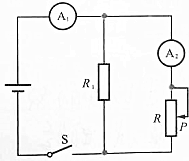

| A. | A1、A2的示数同时增大,同时减小 | |
| B. | A1的示数增加时A2的示数减小,A1的示数减小时A2的示数增大 | |
| C. | A1的示数总大于A2的示数 | |
| D. | A1、A2示数的大小关系无法确定 |



 如图所示,A、B两辆车相距 s=11m,A车以vA=4m/s的速度向右匀速运动,而B车此时的速度vB=10m/s,向右以加速度2m/s2刹车,那么A车追上B车所用的时间为9s.
如图所示,A、B两辆车相距 s=11m,A车以vA=4m/s的速度向右匀速运动,而B车此时的速度vB=10m/s,向右以加速度2m/s2刹车,那么A车追上B车所用的时间为9s.