题目内容
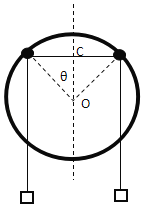
【题目】如图所示，半径为R、圆心为O的大圆环固定在竖直平面内，两个轻质小圆环固定在大圆环上竖直对称轴的两侧θ=45°的位置上，一根轻质长绳穿过两个小圆环，它的两端都系上质量为m的重物，小圆环的大小、绳子与大、小圆环间的摩擦均可忽略．当在两个小圆环间绳子的中点C处，挂上一个质量M的重物，M恰好在圆心处处于平衡．（重力加速度为g）求：
（1）M与m质量之比．
（2）再将重物M托到绳子的水平中点C处，然后无初速释放重物M，则重物M到达圆心处的速度是多大？
【答案】（1）
（2）
【解析】(1)以M为研究对象，受力分析：Mg=2mgcos450
(2)M与2个m组成的系统机械能守恒：
MgRsinθ-2mg(R-Rcosθ)= 
MV12+
mV22
V2=V1cosθ
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
