题目内容
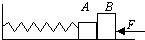如图所示，物体A、B的质量分别为2kg和4kg，位于粗糙的水平桌面上，A、B与桌面间的动摩擦因数均为0.1，劲度系数为200N/m的弹簧一端固定于竖直墙上，另一端固定在A物体上，弹簧原长为20cm，用水平力F推B，平衡时弹簧长度为16cm，水平力F的最小值是2
2
N．如果此时把F改为一水平向右的拉力F?=3N，则B运动3.25
3.25
cm 后A、B开始分离．分析：平衡时，当AB与地面间的静摩擦力到达最大时，F所用的力最小．根据胡克定律和平衡条件求得F的最小值．
当把F改为一水平向右的拉力F′=3N时，两个物体向右加速运动，当两者之间的弹力恰好为零时，将要分离，根据牛顿第二定律和胡克定律列式求解B运动的距离．
当把F改为一水平向右的拉力F′=3N时，两个物体向右加速运动，当两者之间的弹力恰好为零时，将要分离，根据牛顿第二定律和胡克定律列式求解B运动的距离．
解答：解：平衡时，F用力最小时，AB所受地面的静摩擦力向左达到最大，则根据胡克定律和平衡条件得：
Fmin+μ（mA+mB）g=kx
所以 Fmin=kx-μ（mA+mB）g=200×0.04-0.1×6×10=2N
设A、B刚开始分离时，弹簧的压缩量为x′，此时A、B间作用力为零，则
根据牛顿第二定律得：
对B：F′-μmBg=mBa
对A：kx′-μmAg=mAa
联立解得，x′=0.75cm
故B运动的距离为s=4cm-0.75cm=3.25cm
故答案为：2N； 3.25
Fmin+μ（mA+mB）g=kx
所以 Fmin=kx-μ（mA+mB）g=200×0.04-0.1×6×10=2N
设A、B刚开始分离时，弹簧的压缩量为x′，此时A、B间作用力为零，则
根据牛顿第二定律得：
对B：F′-μmBg=mBa
对A：kx′-μmAg=mAa
联立解得，x′=0.75cm
故B运动的距离为s=4cm-0.75cm=3.25cm
故答案为：2N； 3.25
点评：本题关键要分析物体的受力情况，把握住两个物体刚好分享时，相互作用力为零，运用牛顿第二定律求得．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图所示，物体A和B的质量均为m，且分别与跨过定滑轮的轻绳连接（不计绳与滑轮、滑轮与轴之间的摩擦）在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中，则（ ）
如图所示，物体A、B叠放在倾角θ=37°的斜面上，并通过跨过光滑滑轮的细线相连，细线与斜面平行．两物体的质量分别mA=2kg，mB=1kg，A、B间动摩擦因数μ1=0.1，B与斜面间的动摩擦因数μ2=0.2，问：为使A能平行于斜面向下做匀速运动，应对A施加一平行于斜面向下的多大的拉力？
如图所示，物体A和B一起沿斜面匀速下滑，则物体A受到的力是（ ）
如图所示，物体A、B 叠放在光滑的水平地面上mA=1kg，mB=2kg，A、B问最大静摩擦力为6N，用水平推力F推A，为使A、B不产生相对滑动，F最大为如图所示，物体A和B相对静止，以共同的速度沿斜面匀速下滑，则（ ）
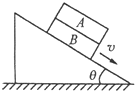
| A、A、B间无摩擦力的作用 | B、B受到滑动摩擦力的大小为（mA+mB）gsinθ | C、B受到静摩擦力的大小为mAgsinθ | D、A物体受到的合力沿斜面向下 |