��Ŀ����
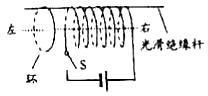
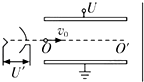
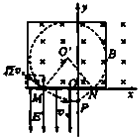
����Ŀ������ϸ�ߵ���һ����Ϊm=0.64kg���߳�ΪL=0.8m�ĵ�����������Ȧabcd����Ȧ�ܵ���ΪR=1�����߳�Ϊd=0.4m�������δų�����ԳƷֲ�����Ȧ�±ߵ����࣬��ͼ���ף���ʾ���ų�����ֱֽ������Ÿ�Ӧǿ�ȴ�С��ʱ��仯��ͼ���ң���ʾ����t=0��ʼ��t0ʱ��ϸ�߿�ʼ�ɳڣ�ȡg=10m/s2 �� ��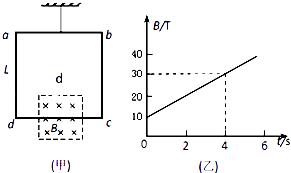
��1����Ȧabcd�в����ĸ�Ӧ�綯��E�͵繦��P��
��2����t0��ֵ��
���𰸡�
��1���⣺�ɷ����ڵ�Ÿ�Ӧ����E= ![]()
����= ![]()
����ͼ��
![]() =5T/s
=5T/s
��ã�E=0.4V
������P= ![]()
��P=0.16W
����Ȧabcd�в����ĸ�Ӧ�綯��0.4V�͵繦��0.16W
��2���⣺��t0ʱ��mg=BId
�����ݱպϵ�·ŷķ���ɣ�I= ![]()
����ͼ��B=10+5t0��
��ã�t0=6s
����t0��ֵ6s
����������1�����ݴŸ�Ӧǿ�ȵı仯�������Ч��������ͨ���ı仯�������ݷ����ڵ�Ÿ�Ӧ���������Ӧ�綯�ƵĴ�С������P=I2R�����Ȧabcd�ĵ繦�ʣ���2����ϸ�߿�ʼ�ɳڣ��߿��������Ͱ�����ƽ�⣬����ƽ������Ÿ�Ӧǿ�ȵĴ�С���Ӷ����ͼ�����������ʱ�䣮
�����㾫�������յ�Ÿ�Ӧ����ѧ�ǽ����ĸ�������Ҫ֪���÷����ڵ�Ÿ�Ӧ���ɺ���ζ������Ӧ�綯�ƵĴ�С�ͷ������·�е���ǿ�ȣ������о�������������������������������ֶ���ȷ���䷽���ж���ѧ���̻�ƽ�ⷽ����⣮

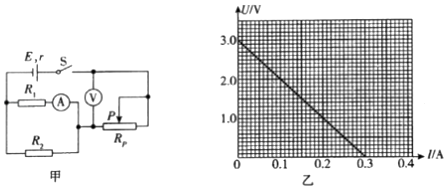
����Ŀ��ijʵ��С��������ͼ����ʾ�ĵ�·�о�����3.5V������������ּ����壩��С���ݵķ������ԣ�
��1������ݵ�·ͼ��ͼ������ȱ�ĵ��߲������� �� Ϊ�˱�֤ʵ��İ�ȫ��������ͷ��ʵ�鿪ʼǰӦ���ڻ��������������ˣ���ѡ����ҡ���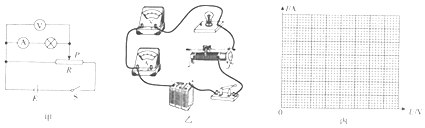
��2��ʵ��õ���8���������±�������ͼ����ѡ����ʵı������I��Uͼ��
I/A | 0 | 0.100 | 0.151 | 0.172 | 0.202 | 0.210 | 0.219 | 0.222 |
U/V | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
��3��ʵ����С�������˵�ѹ����仯�����ѹ�Ĺ����У�С����������ֵԼΪ����������������λ��Ч���֣���ϵͳ����ʹ����������ƫ��ƫС������