题目内容
在探究某种笔的弹跳问题时,建立以下简化模型进行研究。
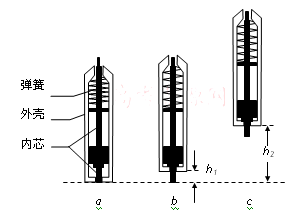
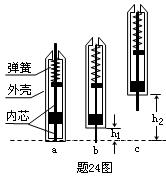
把笔分为轻质弹簧、圆筒和直杆三部分,薄挡板P固定在直杆上,轻质弹簧的两端分别固定在圆筒顶部和薄挡板P上,质量为M的圆筒可沿直杆无摩擦滑动,直杆和挡板P的总质量为m。开始时将笔直立于水平桌面,在桌面上方的矩形区域内有竖直向上的匀强电场,带正电的挡板P非常靠近电场的上边界,挡板P与周围物体绝缘接触,受到的电场力与笔的重力大小相等。向上移动圆筒使弹簧处于原长状态,此时挡板P刚好与圆筒底部接触,如图甲所示。现用力缓慢向下压圆筒,使圆筒底部恰好与水平桌面接触,此过程中压力做功为W,如图乙所示。撤除压力,圆筒弹起并与挡板P碰撞,两者一起上升到最大高度后自由落下,此后直杆在桌面上多次跳动。
假设圆筒与挡板P每次碰撞结束时均具有相同速度,碰撞时间均忽略不计。直杆与桌面每次碰撞后均不反弹,直杆始终保持竖直状态。不计一切摩擦与空气阻力,重力加速度大小为g,求:
(1)直杆第一次上升的最大高度h1;
(2)直杆运动的总路程h。

解答:
(1)设将圆筒下移h0,设其底部与水平桌面接触时,弹簧的弹性势能为EP,
根据功能关系
![]() ① 2分
① 2分
撤除压力后,当弹簧恢复原长时,设圆筒与挡板碰前的速度为v0,
根据能量守恒
![]() ② 2分
② 2分
联立①②解得 ![]() ③
③
设圆筒与直杆碰撞后共同速度为v1,
由动量守恒定律 Mv0=(M+m)v1 ④ 2分
此后圆筒与杆共同做竖直上抛运动 ![]() ⑤2分
⑤2分
联立③④⑤解得 h1=![]() ⑥ 2分
⑥ 2分
(2)由于![]() ,所以此后圆筒底部不再与水平桌面接触。
,所以此后圆筒底部不再与水平桌面接触。
根据机械能守恒,圆筒底部与挡板第二次碰前瞬间的速度为v1,
设碰后共同速度为v2,由于笔所受电场力与重力平衡,
根据动量守恒定律
![]() 即
即![]() ⑦ 1分
⑦ 1分
直杆第2次上升的最大高度 ![]() ⑧ 1分
⑧ 1分
同理可得,圆筒底部与挡板第n次碰后速度
![]() ⑨ 2分
⑨ 2分
直杆第n次上升的最大高度 ![]() ⑩ 2分
⑩ 2分
故直杆运动的总路程为 ![]()
![]() (11)2分
(11)2分
联立解得 ![]()
![]() 2分
2分

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
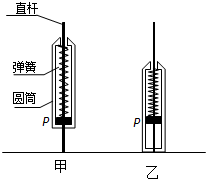 (2010?武汉二模)在探究某种笔的弹跳问题时,建立以下简化模型进行研究.
(2010?武汉二模)在探究某种笔的弹跳问题时,建立以下简化模型进行研究.