Question

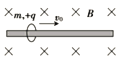
【题目】m1和m2两物体与斜面之间的滑动摩擦因数相同，已知m1＞m2 ， 它们先后从同一斜面的顶端由静止开始自由下滑，则它们到达底端的速度（　　）
A.v1＞v2
B.v1=v2
C.v1＜v2
D.不确定

Answer 1

【答案】B
【解析】解：设斜面的长度为L，斜面的倾角为θ，任一物体质量为m，加速度为a，根据牛顿第二定律得：

mgsinθ﹣f=ma

N﹣mgcosθ=0，

又f=μN

联立三式解得 a=gsinθ﹣μgcosθ

物体沿斜面做匀加速运动，由v2=2aL得：

物体到达底端的速度 v= = ，与物体的质量无关，则有v1=v2．

故选：B

【考点精析】本题主要考查了自由落体运动的相关知识点，需要掌握（1）条件:初速度为零，只受重力作用；（2）性质:是一种初速为零的匀加速直线运动，a=g才能正确解答此题．