题目内容
15.一个质点从静止开始做匀加速直线运动,它在第2s内与第4s内通过的位移之比为x1:x2,通过第1m与通过第3m时的平均速度之比为 v1:v2,则( )| A. | x1:x2=5:11,v1:v2=1:$\sqrt{2}$ | B. | x1:x2=1:4,v1:v2=1:$\sqrt{2}$ | ||
| C. | x1:x2=3:7,v1:v2=($\sqrt{2}+\sqrt{3}$):1 | D. | x1:x2=3:7,v1:v2=($\sqrt{3}-\sqrt{2}$):1 |
分析 根据初速度为零的匀加速直线运动的推论得出第1s内、第2s内、第3s内的…的位移之比,以及在相等位移内所用的时间之比,从而求出在第2s内与第4s内通过的位移之比,通过第1m与通过第3m时的平均速度之比.
解答 解:初速度为零的匀加速直线运动的推论得出第1s内、第2s内、第3s内、第4s内的…的位移之比为1:3:5:7:…,
则第2s内与第4s内通过的位移之比为:x1:x2=3:7.
初速度为零的匀加速直线运动在连续相等位移内所用的时间之比为$1:(\sqrt{2}-1):(\sqrt{3}-\sqrt{2}):$…,
则通过第1m和第3m所用的时间之比为1:$(\sqrt{3}-\sqrt{2})$,
根据平均速度的定义式知,${v}_{1}:{v}_{2}=1:\frac{1}{\sqrt{3}-\sqrt{2}}=(\sqrt{3}-\sqrt{2}):1$,故ABC错误,D正确.
故选:D.
点评 本题考查了初速度为零的匀加速度直线运动,知道连续相等时间内的位移之比以及通过相等位移内的时间之比这些结论,对本题的解答很有帮助.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
7.电流表的内阻是Rg=200Ω,满刻度电流值是Ig=500 μA,现欲把这电流表改装成量程为2.0V的电压表,正确的方法是( )
| A. | 应串联一个0.05Ω的电阻 | B. | 应并联一个0.05Ω的电阻 | ||
| C. | 应串联一个3 800Ω的电阻 | D. | 应并联一个3 800Ω的电阻 |
6.下列关于力、功、能的关系正确的是( )
| A. | 外力F对物体系某物体做正功,则该系统的某种能量可能增加 | |
| B. | 物体所受的重力做正功,该物体的动能一定增加 | |
| C. | 物体所受合外力对该物体做正功,该物体动能一定增加 | |
| D. | 系统内某物体所受合外力做功为零,则该系统的机械能一定守恒 |
3.一个小球从距地面4m高处竖直向下抛出,被地面弹回后在距地面1m高处被接住,坐标原点定在抛出点正下方2m处,选向下方向为坐标轴的正方向,抛出点、落地点、接住点的位置坐标分别为( )
| A. | 2m,-2m,-1m | B. | -2m,2m,1m | C. | 4m,0m,1m | D. | -2m,0m,-1m |
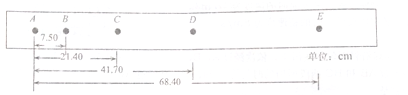
7. 如图所示,光滑斜面被分成四个长度相等的部分,一个物体由A点静止释放,下面结论中错误的是( )
如图所示,光滑斜面被分成四个长度相等的部分,一个物体由A点静止释放,下面结论中错误的是( )
 如图所示,光滑斜面被分成四个长度相等的部分,一个物体由A点静止释放,下面结论中错误的是( )
如图所示,光滑斜面被分成四个长度相等的部分,一个物体由A点静止释放,下面结论中错误的是( )| A. | 物体到达各点的速度vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点所经历的时间tB:tC:tD:tE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 物体从A到E的平均速度$\overline{v}$=vB | |
| D. | 通过四段长度相等的每一部分时,其速度增量均相等 |
 在如图中,E=3.5V,r=1Ω,R1=R2=4Ω,R3=2Ω,则当K1、K2都接通时,R1上消耗的功率与K2接通K1断开时,R1上消耗功率之比为49:100.
在如图中,E=3.5V,r=1Ω,R1=R2=4Ω,R3=2Ω,则当K1、K2都接通时,R1上消耗的功率与K2接通K1断开时,R1上消耗功率之比为49:100.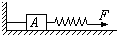 如图所示,放在水平地面上的物体A 重G=100N,左侧用轻质绳系在墙上,此时张力为零,右侧连着一轻质弹簧,已知物体与地面间的动摩擦因数μ=0.4,可认为物体所受的最大静摩擦力等于滑动摩擦力.弹簧的劲度系数k=2500N/m.在弹簧的右端加一水平拉力 F,则:
如图所示,放在水平地面上的物体A 重G=100N,左侧用轻质绳系在墙上,此时张力为零,右侧连着一轻质弹簧,已知物体与地面间的动摩擦因数μ=0.4,可认为物体所受的最大静摩擦力等于滑动摩擦力.弹簧的劲度系数k=2500N/m.在弹簧的右端加一水平拉力 F,则: