题目内容
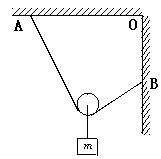
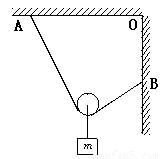
(1)如图所示,将一条轻而柔软的细绳一端固定在天花板上的A点,另一端固定在竖直墙上的B点,A和B到O点的距离相等,绳长为OA的两倍.滑轮的大小与质量均可忽略,滑轮下悬挂一质量为m的重物.设摩擦力可忽略,求平衡时绳所受的拉力为多大?
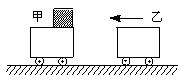
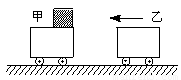
(2)如图所示,甲车的质量是2 kg,静止在光滑水平面上,上表面光滑,右端放一个质量为1 kg的小物体.乙车质量为4 kg,以5 m/s的速度向左运动,与甲车碰撞以后甲车获得8 m/s的速度,物体滑到乙车上.若乙车足够长,上表面与物体的动摩擦因数为0.2,则物体在乙车上表面滑行多长时间相对乙车静止?(g取10 m/s2)


(1)T=![]() mg
mg
(2)t=0.4 s
解析:
(1)如右图所示:由平衡条件得
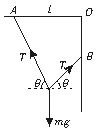
2Tsinθ=mg
设左、右两侧绳长分别为l1、l2,AO=l,则由几何关系得
l1cosθ+l2cosθ=l
l1+l2=2l
由以上几式解得θ=60°
T=![]() mg
mg
(2)乙与甲碰撞动量守恒:
m乙v乙=m乙v乙′+m甲v甲′
小物体m在乙上滑动至有共同速度v,对小物体与乙车运用动量守恒定律得?
m乙v乙′=(m+m乙)v
对小物体应用牛顿第二定律得a=μg
所以t=v/μg
代入数据得t=0.4 s

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则( )
如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则( )