题目内容
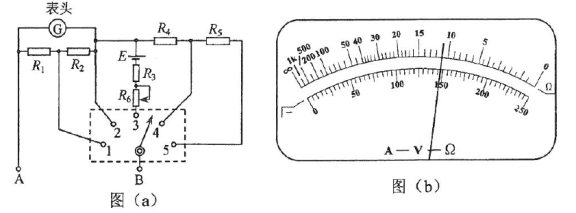
【题目】摄制组在某大楼边拍摄武打片，要求特技演员从地面飞到屋顶．为此导演在某房顶离地H=8m处架设了轮轴，如图所示，轮和轴的直径之比为3:1，特技演员的质量m=60kg，若轨道车从图中A前进s=6m到B处时速度为v=5m/s，人和车可视为质点，轮轴的质量不计，轮轴的大小相对于H可忽略，g取10m/s2.则这一过程中 ( )
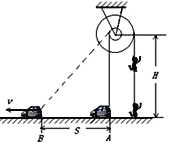
A. 演员上升的高度h=2m
B. 演员上升的高度h=6m
C. 演员的速度变化量是9m/s
D. 钢丝对演员做的功W=3870 J
【答案】BC
【解析】由图可知，在这一过程中，连接轨道车的钢丝上升的距离为
,轮和轴的直径之比为3：1．所以演员上升的距离为h=3×2m=6m．故A错误，B正确．将汽车的速度v分解，则得绳子的伸长速度v1=vcos53°=5×0.6=3m/s，由于轮轴的角速度相等．设人的上升速度为v3，轮的半径为R，轴的半径为r，则有
，得
，故C正确；由动能定理可知，钢丝对演员做的功
，故D错误；故选BC．
练习册系列答案
相关题目
