题目内容
【题目】如图，倾角为θ=37°的足够长的斜面上，有一质量为M=1.0kg，长为L=2.55m的薄板A。薄板A由两种不同材料拼接而成，其上表面以ab为分界线，其中ab以上部分光滑，长度为L1＝0.75m，下表面与斜面间的动摩擦因数μ1＝0.4。在薄板A的上表面上端放一质量m=1.0kg的小物块B(可视为质点）。同时将A、B由静止释放，已知B与A的上表面ab以下部分的动摩擦因数μ2＝0.25，B与斜面间的动摩擦因数μ3＝0.5,认为滑动摩擦力与最大静摩擦力大小相等．物块B从薄板A上滑到斜面上时速度不变。取g＝10m/s2，sin37°＝0.6。求：
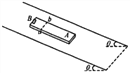
(1)B从开始滑动到刚经过ab时所用的时间；
(2)B在A上滑动的总时间；
(3)从A、B分离到A在斜面上追上B所用的时间。
【答案】(1)t1=0.5s （2）t=1s （3）t3=10.5s
【解析】(1)对物块B：设刚释放时其加速度为a1．
mgsinθ=m a1
对木板A：Mgsinθ<μ1(m+M)gcosθ
这说明B在A的光滑部分滑动时，A保持静止．
设B刚离开A的光滑部分时速度为v1：v12=2a1L1
解得：v 1=3m/s
B在A的光滑部分滑动的时间为t 1：v1=a1t1
解得：t1=0.5s
(2)B在A的粗糙部分滑动时，设B的加速度为a2，A的加速度为a3，该过程所用的时间为t2，B的位移为x1，A的位移为x2．
解得：
=4m/s2，
=1.6m/s2
解得：t2=0.5s
B在A上滑动的总时间为t：t=t1+t2=1s
(3)设B离开薄板A时，B和薄板A的速度分别为v2和v3．
解得：
m/s
m/s
B滑到斜面上后，设B的加速度为a4，A的加速度为a5．
解得：a4=2m/s2，a5=2.8m/s2
设B滑到斜面上后到A、B再次相遇所用的时间为t3，所运动的位移为x3．
解得：t3=10.5s
