题目内容
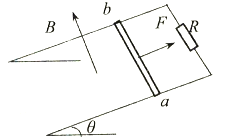
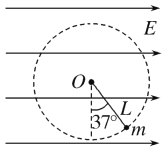
【题目】在水平地面上放一木板B,重力为G2=100N,再在木板上放一货箱A,重力为G1=500N,设货箱与木板、木板与地面的动摩擦因数μ均为0.5,先用绳子把货箱与墙拉紧,如图所示,已知tanθ=3/4,然后在木板上施一水平力F,想把木板从货箱下抽出来,F至少应为多大?

【答案】413.6N
【解析】
当木板刚要从货箱下抽出来,B与A和地面间的静摩擦力达到最大值,此时F最小.先以A为研究对象,分析受力情况,根据平衡条件求出B对A的支持力和摩擦力,再以B为研究对象,分析受力情况,根据平衡条件求出F.
以A为研究对象,物体的受力图如图,根据平衡条件得:
Tcosθ=f
N+Tsinθ=G1
又f=μN
得N=363.64N,f=181.81N

再以B为研究对象,分析受力得知,B水平方向受到拉力、A对B水平向右的摩擦力f′和地面对B水平向右的摩擦力f1.根据牛顿第三定律得:f′=f=181.81N
由平衡条件得:
N1=N′+G2
Fmin=f′+f1
其中N′=N,f1=μN1=μ(N+G2)=231.81N
解得:Fmin=413.6N

练习册系列答案
相关题目