题目内容
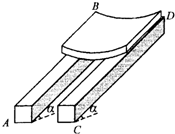（2008?福建模拟）某建筑工地的工人为了运送瓦片，用两根截面为正方形的木料AB、CD，支在水平地面上形成斜面，AB与CD平行且与地面有相同的倾角α，如图所示．从斜面上端将几块瓦片叠放在一起无初速释放，让瓦片沿木料下滑到地面（瓦片截面可视为一段圆弧），现发现因滑到地面时速度过大而造成瓦片破裂．为了不使瓦片破裂，在不改变斜面倾角α的前提下，可以采取的措施是（ ）分析：因滑到地面时速度过大而造成瓦片破裂．为了不使瓦片破裂，是因为瓦片做匀加速运动造成的，若加速度减小，则相应的瓦到地面的速度也减小，可防止瓦片破裂．在不改变斜面倾角α的前提下，可以看受力与那些因素有关，由牛顿第二定律得到加速度，从而判定可行的措施．
解答：解：
A、B、保持装置不变，而改变瓦片的块数，由瓦片的受重力，摩擦力，支持力，设杆对瓦的支持力的方向与杆的垂线的夹角为β，则：
在沿瓦片的半径方向：mgcosα=2Ncosβ
在运动方向上由牛顿第二定律：mgsinα-2μN=ma
解得：a=
=gsinα-
由于不改变斜面倾角α，可知，加速与瓦片块数无关，增减瓦片的块数无法改变加速度，也就改变不了瓦片到地面的速度，仍会因到地面速度过大而造成瓦片破裂，故A错误，B错误．
C、D、由上面的计算结果可知，在固定斜面倾角α的前提下，要改变加速度，只能改变杆对瓦的支持力与杆垂线的夹角β．为使瓦匀速运动，必须有：a=0，
即cosβ减小，则β角要增大，故应把两根木料往两侧分开一些，故C错，D正确．
故选：D．
A、B、保持装置不变，而改变瓦片的块数，由瓦片的受重力，摩擦力，支持力，设杆对瓦的支持力的方向与杆的垂线的夹角为β，则：
在沿瓦片的半径方向：mgcosα=2Ncosβ
在运动方向上由牛顿第二定律：mgsinα-2μN=ma
解得：a=
mgsinα-
| ||
| m |
| μgcosα |
| cosβ |
由于不改变斜面倾角α，可知，加速与瓦片块数无关，增减瓦片的块数无法改变加速度，也就改变不了瓦片到地面的速度，仍会因到地面速度过大而造成瓦片破裂，故A错误，B错误．
C、D、由上面的计算结果可知，在固定斜面倾角α的前提下，要改变加速度，只能改变杆对瓦的支持力与杆垂线的夹角β．为使瓦匀速运动，必须有：a=0，
即cosβ减小，则β角要增大，故应把两根木料往两侧分开一些，故C错，D正确．
故选：D．
点评：本题主要是理清思路：瓦片是因速度过大而破裂，则要想不破裂就需要落地速度减小，而速度是与加速度有关的，由牛顿第二定律可以得到加速度的表达式，进而我们就可以找到防止瓦片破裂的方法．本题题目不大，但是难度不小，若平时思维条理训练不足，难以解答本题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2008?福建模拟）“嫦娥二号”已于2010年10月1日发射，其环月飞行的高度距离月球表面100km，所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加翔实．若两颗卫星环月的运行均可视为匀速圆周运动，运行轨道如图所示．则（ ）
（2008?福建模拟）滑板运动是一项陆地上的“冲浪运动”滑板运动员可在不同的滑坡上滑行，做出各种动作，给人以美的享受．如图甲所示，abcdef为同一竖直平面上依次平滑连接的滑行轨道，其中ab段水平，H=3m，bc段和cd段均为斜直轨道，倾角θ=370，de段是一半径R=2.5m的四分之一圆弧轨道，0点为圆心，其正上方的d点为圆弧的最高点．滑板及运动员的总质量m=60kg，运动员滑经d点时轨道对滑板支持力用Nd表示．忽略摩擦阻力和空气阻力，取g=10m/s2，sin 37°=0.6，eos 37°=0.8．除下述问题（3）中运动员做缓冲动作以外，均可把滑板及运动员视为质点．
（2008?福建模拟）如图所示，在NOQ范围内有垂直于纸面向里的匀强磁场I，在MOQ范围内有垂直于纸面向外的匀强磁场Ⅱ，M、O、N在一条直线上，∠MOQ=60°，这两个区域磁场的磁感应强度大小均为B．离子源中的离子带电荷量为+q，质量为m，通过小孔O1进入两板间电压为U的加速电场区域（可认为初速度为零），离子经电场加速后由小孔O2射出，再从O点进入磁场区域I，此时速度方向沿纸面垂直于磁场边界MN不计离子的重力．
（2008?福建模拟）两滑杆上分别套A、B两圆环，两环上分别用细线悬吊着两物体C、D，如图所示，当它们都沿滑杆向下滑动时，A的悬线始终与杆垂直，B的悬线始终竖直向下．则（ ）