题目内容
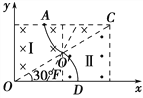
【题目】如图所示，在直角坐标系xOy的第一象限中两个相同的直角三角形区域Ⅰ、Ⅱ内分别充满了方向相反、磁感应强度大小均为B的匀强磁场，已知C点坐标为(
，l)，质量为m，带电荷量为q的正电荷从A(
，l)点以一定的速度平行于y方向垂直进入磁场，并从x轴上的D点(图中未画出)垂直x轴离开磁场，电荷重力不计。
(1)求D点的位置坐标及电荷进入磁场区域Ⅰ时的速度大小v；
(2)若将区域Ⅱ内的磁场换成沿－x轴方向的匀强电场，该粒子仍从A点以原速度进入磁场区域Ⅰ，并最终仍能垂直x轴离开，求匀强电场的场强E。
【答案】(1)
(2)
【解析】
(1)根据粒子运动的对称性可知，粒子从OC的中点O′进入磁场区域Ⅱ，且AC＝OD，则D的坐标为(
l，0)。设粒子在磁场中运动的半径为r，在磁场Ⅰ中的轨迹所对圆心角为θ，
根据几何知识可知rsin θ＝
l，
r－rcos θ＝
l－
l，
解得θ＝
，r＝l。
粒子在磁场中做圆周运动，qvB＝m
，
速度大小
，
故
(2)设粒子在电场中的运动时间为t，加速度大小为a，
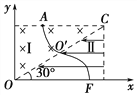
则根据运动的分解可知，在x轴方向：0－vsin θ＝－at，
在y轴方向：vtcos θ＝l，其中，qE＝ma，
联立解得:
【题目】如图为“探究物体的加速度与质量和受力的关系”的实验装置。沙和沙桶的质量为m，小车和砝码的质量为M。实验中将沙和沙桶的重力作为细线对小车的拉力。
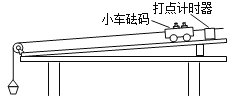
（1）实验前，在进行平衡摩擦力的操作时，下列注意事项正确的是
A．应该让小车连接纸带并穿过打点计时器 |
B．必须让小车连接沙桶 |
C．纸带和沙桶都应连接 |
D．纸带和沙桶都不能连接 |
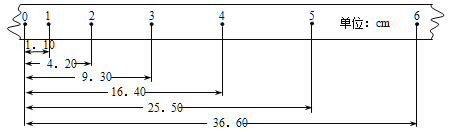
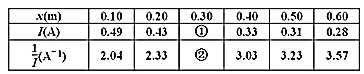
（2）现保持沙和沙桶的总质量m不变，改变小车和砝码的总质量M，探究加速度和质量的关系。如图是某次实验中打出的一条纸带，交变电流的频率为50Hz，每隔4个点选一个计数点，则小车的加速度为____m/s2（保留两位有效数字）。通过实验得到多组加速度a、质量M的数据，为了方便准确地研究二者关系，一般选用纵坐标为加速度a，则横坐标为__ __（填M或
）。
