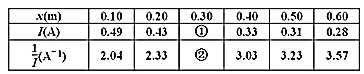
题目内容
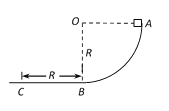
【题目】如图所示,竖直平面内有一半径为R的固定四分之一圆轨道与水平轨道相切于最低点B.一质量为m的小物块P(可视为质点)从A处由静止滑下,经过最低点B后沿水平轨道运动,到C处停下,B、C两点间的距离为R,物块P与圆轨道、水平轨道之间的动摩擦因数均为μ。若将物块P从A处正上方离A高度为R处由静止释放后,从A处进入轨道,最终停在水平轨道上D点,B、D两点间的距离为s,下列关系正确的是 ( )
A. s < (1 +![]() )R B. s = (1 +
)R B. s = (1 +![]() )R
)R
C. s< (1-![]() )R D. s = 2R
)R D. s = 2R
【答案】A
【解析】小物块从A处由静止滑下,经过最低点B后沿水平轨道运动,到C处停下,根据动能定理得:mgR-Wf-μmgR=0,若物块P从A处正上方高度为R处静止释放,从A处进入轨道,最终停在水平轨道上D点,根据动能定理得:mg2R-Wf′-μmgs=0,若Wf=Wf′,则![]() ,由于第二次经过圆弧轨道的速度较大,根据径向的合力提供向心力知,压力较大,摩擦力较大,所以Wf′>Wf,可知
,由于第二次经过圆弧轨道的速度较大,根据径向的合力提供向心力知,压力较大,摩擦力较大,所以Wf′>Wf,可知![]() ,故A正确,BCD错误。
,故A正确,BCD错误。

练习册系列答案
相关题目