题目内容
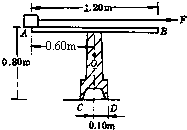 质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?分析:设当铁块运动到E点时,支架刚好开始转动,此时过E点的竖直线在D点左侧,距D点为S,根据杠杆平衡条件及已知条即可求解出S;然后对滑块,根据牛顿第二定律求解出加速度后运用位移时间关系公式求解时间.
解答:解:当导轨刚要不能维持平衡时,C端受的力为零,此时导轨(及支架)受四个力作用:滑块对导轨的压力FN=mg,竖直向下,滑块对导轨的摩擦力Ff=μmg=10N,重力G=m′g,作用在O点,方向竖直向下,作用于轴D端的力.
设此时的铁块走过的路程S,根据有固定转动轴物体平衡条件及图中尺寸,有:
m′g×0.1+mg(0.7-s)=Ff×0.8=μmg×0.8
代入数据,有:40×0.1+20(0.7-s)=10×0.8
解得s=0.5m
铁块受的摩擦力Ff=10N,方向向右.
根据牛顿第二定律,有:F-Ff=ma
解得:a=1.0m/s2
∵S=
at2
∴t=1.0s
答:从小铁块运动时起,导轨(及支架)能保持静止的最长时间是1s.
设此时的铁块走过的路程S,根据有固定转动轴物体平衡条件及图中尺寸,有:
m′g×0.1+mg(0.7-s)=Ff×0.8=μmg×0.8
代入数据,有:40×0.1+20(0.7-s)=10×0.8
解得s=0.5m
铁块受的摩擦力Ff=10N,方向向右.
根据牛顿第二定律,有:F-Ff=ma
解得:a=1.0m/s2
∵S=
| 1 |
| 2 |
∴t=1.0s
答:从小铁块运动时起,导轨(及支架)能保持静止的最长时间是1s.
点评:此题考查的知识点较多,由牛顿第二定律的应用、位移的计算,杠杆平衡条件等一系列知识点,此题将这些知识点综合起来,提高了学生用物理知识和规律解决问题的能力,因此是一道好题.

练习册系列答案
相关题目
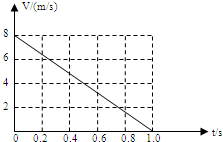 一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的V-t时间图线,如图所示.(取sin37°=0.6 cos37°=0.8 g=10m/s2)求:
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的V-t时间图线,如图所示.(取sin37°=0.6 cos37°=0.8 g=10m/s2)求: (2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
(2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为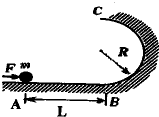 如图所示,光滑水平面右端B处连接一个竖直的半径为R=0.4m的光滑半圆形轨道,B点为水平面与轨道的切点,用水平恒力F将质量m=2.0kg的小球从A点由静止开始推到B点后撤去恒力,AB间距离为L.(小球大小可以忽略,g=10m/s2)
如图所示,光滑水平面右端B处连接一个竖直的半径为R=0.4m的光滑半圆形轨道,B点为水平面与轨道的切点,用水平恒力F将质量m=2.0kg的小球从A点由静止开始推到B点后撤去恒力,AB间距离为L.(小球大小可以忽略,g=10m/s2)
 如图,质量m=2.0kg的滑块(可视为质点)放在水平面上,与水平面之间的动摩擦因数μ1=0.2,质量也为m=2.0kg的无底盒盖住滑块,盒长L=20cm,盒子与地面动摩擦因数μ2=0.1.现给盒子一个水平向右的初速度v0=10m/s,若盒子与滑块的碰撞是弹性的,试讨论盒子与滑块的碰撞次数.
如图,质量m=2.0kg的滑块(可视为质点)放在水平面上,与水平面之间的动摩擦因数μ1=0.2,质量也为m=2.0kg的无底盒盖住滑块,盒长L=20cm,盒子与地面动摩擦因数μ2=0.1.现给盒子一个水平向右的初速度v0=10m/s,若盒子与滑块的碰撞是弹性的,试讨论盒子与滑块的碰撞次数.