题目内容
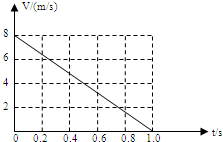一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度，并用计算机做出了小物块上滑过程的V-t时间图线，如图所示．（取sin37°=0.6 cos37°=0.8 g=10m/s2）求：（1）小物块冲上斜面过程中加速度的大小；
（2）小物块与斜面间的动摩擦因数；
（3）小物块返回斜面底端时的速度大小（结果保留一位小数）．
分析：（1）根据匀变速直线运动的速度时间图线求出小物块冲上斜面过程中的加速度大小．
（2）对物体受力分析，根据牛顿第二定律求出支持力和摩擦力的大小，从而求出动摩擦因数．
（3）根据牛顿第二定律求出返回时的加速度，通过图线求出斜面的长度，根据匀变速直线运动的速度位移公式求出小物块返回斜面底端时的速度大小．
（2）对物体受力分析，根据牛顿第二定律求出支持力和摩擦力的大小，从而求出动摩擦因数．
（3）根据牛顿第二定律求出返回时的加速度，通过图线求出斜面的长度，根据匀变速直线运动的速度位移公式求出小物块返回斜面底端时的速度大小．
解答：解：（1）由图线得，a=
m/s2=8m/s2
（2）在垂直于斜面方向上有：FN-mgcosθ=0
沿斜面方向上有：Ff+mgsinθ=ma
Ff=μFN
联立各式解得：?=0.25
（3）小物块上滑距离：
由速度时间图线知，斜面的长度s=
v0t=4m
mgsinθ-μmgcosθ=ma
v2=2as
v=5.7m/s．
答：（1）小物块冲上斜面过程中加速度的大小为8m/s2．
（2）小物块与斜面间的动摩擦因数为0.25．
（3）小物块返回斜面底端时的速度大小为5.7m/s．
| 8.0 |
| 1 |
（2）在垂直于斜面方向上有：FN-mgcosθ=0
沿斜面方向上有：Ff+mgsinθ=ma
Ff=μFN
联立各式解得：?=0.25
（3）小物块上滑距离：
由速度时间图线知，斜面的长度s=
| 1 |
| 2 |
mgsinθ-μmgcosθ=ma
v2=2as
v=5.7m/s．
答：（1）小物块冲上斜面过程中加速度的大小为8m/s2．
（2）小物块与斜面间的动摩擦因数为0.25．
（3）小物块返回斜面底端时的速度大小为5.7m/s．
点评：加速度是联系力学和运动学的桥梁，通过加速度，可以根据力求运动，也可以根据运动求力．
练习册系列答案
名校课堂系列答案
相关题目
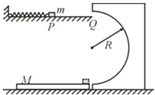如图所示，在水平光滑轨道PQ上有一轻弹簧，其左端固定在竖直墙上，右端与一质量m=2.0kg的小物块（可视为质点）接触，现推动小物块将弹簧压缩后由静止释放，物块被弹簧弹出后沿水平轨道运动至右端沿切线进入竖直固定的半圆轨道，且小物块进入半圆轨道时与轨道间恰无相互作用．小物块沿半圆轨道运动经过最低点后滑上质量M=8.0kg的长木板，最后恰好停在长木板最左端．已知竖直半圆轨道光滑且半径R=0.5m，物块与木板间的动摩擦因数μ=0.2，木板与水平地面间摩擦不计，取g=10m/s2．求：
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用传感器测出了小物块冲上斜面过程中不同时刻的瞬时速度，并用计算机做出了小物块上滑过程的速度一时间图线，如图所示．（取sin37°=0.6，cos37°=0.8，g=10m/s2）求：
（2011?东莞模拟）如图所示，一质量M=2.0kg的长木板静止放在光滑水平面上，在木板的右端放一质量m=1.0kg可看作质点的小物块，小物块与木板间的动摩擦因数为μ=0.2．用恒力F向右拉动木板使木板在水平面上做匀加速直线运动，经过t=1.0s后撤去该恒力，此时小物块恰好运动到距木板右端l=1.0m处．在此后的运动中小物块没有从木板上掉下来．求：
（2011?黄石模拟）如图所示，固定点O上系一长l=0.6m的细绳，细绳的下端系一质量m=1.0kg的小球（可视为质点），原来处于静止状态，球与平台的B点接触但对平台无压力，平台高h=0.80m，一质量M=2.0kg的物块开始静止在平台上的P点，现对M施予一水平向右的瞬时冲量，物块M沿粗糙平台自左向右运动到平台边缘B处与小球m发生正碰，碰后小球m在绳的约束下做圆周运动，经最高点A时，绳上的拉力恰好等于摆球的重力，而M落在水平地面上的C点，其水平位移s=1.2m，不计空气阻力．g=10m/s2．求：