题目内容
 (2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
(2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
|
(1)t=10s时刻物体的位置坐标;
(2)t=10s时刻物体的速度和加速度的大小和方向;
(3)t=10s时刻水平外力的大小.
分析:对照匀速直线运动的位移公式x=vt和匀加速直线运动的位移公式x=v0+
at2,根据物体坐标与时间的关系得到物体在x轴、y轴方向的分速度和加速度,判断出物体的运动性质,将分速度合成得到物体的速度.再利用正交分解,根据牛顿第二定律求出水平外力.
| 1 |
| 2 |
解答: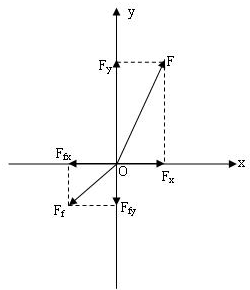 解:(1)x=3t=3×10m=30m y=0.2t2=0.2×102m=20m
解:(1)x=3t=3×10m=30m y=0.2t2=0.2×102m=20m
即t=10s 时刻物体的位置坐标为(30m,20m)
(2)根据x=3t,y=0.2t2判断:物体在x轴方向做匀速直线运动,在y轴方向做初速度为0的匀加速直线运动.
且vx=3m/s,a=0.4m/s2,vy=at=0.4×10m/s=4m/s
则v=
=5m/s
设v方向与x轴正方向夹角为θ
则tanθ=
=
,θ=53°
(3)如图,摩擦力方向与物体运动方向相反,外力与摩擦力的合力使物体加速.
应用正交分解法 Ff=μmg,Ffx=0.6 Ff=0.6N,Ffy=0.8 Ff=0.8N
根据牛顿第二定律,得Fx-Ffx=0,Fx=o,6N
Fy-Ffy=ma,Fy=1.6N
则F=
=1.7N
答:(1)t=10s时刻物体的位置坐标(30m,20m)
(2)t=10s时刻物体的速度的大小为5m/s,方向与x轴正方向夹角为53°;加速度的大小为0.4m/s2,方向为y轴正方向.
(3)t=10s时刻水平外力的大小为1.7N.
 解:(1)x=3t=3×10m=30m y=0.2t2=0.2×102m=20m
解:(1)x=3t=3×10m=30m y=0.2t2=0.2×102m=20m即t=10s 时刻物体的位置坐标为(30m,20m)
(2)根据x=3t,y=0.2t2判断:物体在x轴方向做匀速直线运动,在y轴方向做初速度为0的匀加速直线运动.
且vx=3m/s,a=0.4m/s2,vy=at=0.4×10m/s=4m/s
则v=
|
设v方向与x轴正方向夹角为θ
则tanθ=
| vy |
| vx |
| 4 |
| 3 |
(3)如图,摩擦力方向与物体运动方向相反,外力与摩擦力的合力使物体加速.
应用正交分解法 Ff=μmg,Ffx=0.6 Ff=0.6N,Ffy=0.8 Ff=0.8N
根据牛顿第二定律,得Fx-Ffx=0,Fx=o,6N
Fy-Ffy=ma,Fy=1.6N
则F=
| Fx+Fy |
答:(1)t=10s时刻物体的位置坐标(30m,20m)
(2)t=10s时刻物体的速度的大小为5m/s,方向与x轴正方向夹角为53°;加速度的大小为0.4m/s2,方向为y轴正方向.
(3)t=10s时刻水平外力的大小为1.7N.
点评:本题的技巧是运用正交分解法研究方向未知的外力,这是物理上常用的方法,求其他量同样可以参考应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013?商丘二模)把电阻非线性变化的滑动变阻器接入图1的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压与x间的关系如图2,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( )
(2013?商丘二模)把电阻非线性变化的滑动变阻器接入图1的电路中,移动滑动变阻器触头改变接入电路中的长度x(x为图中a与触头之间的距离),定值电阻R1两端的电压与x间的关系如图2,a、b、c为滑动变阻器上等间距的三个点,当触头从a移到b和从b移到c的这两过程中,下列说法正确的是( ) (2013?商丘二模)如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知点a电势为20V,b点电势为24V,d点电势为12V.一个质子从b点以v0的速度射入此电场,入射方向与bc成450,一段时间后经过c点.不计质子的重力.下列判断正确的是( )
(2013?商丘二模)如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知点a电势为20V,b点电势为24V,d点电势为12V.一个质子从b点以v0的速度射入此电场,入射方向与bc成450,一段时间后经过c点.不计质子的重力.下列判断正确的是( ) (2013?商丘二模)质量为m的物块在平行于斜面的力F作用下,从倾角为θ的固定斜面底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则( )
(2013?商丘二模)质量为m的物块在平行于斜面的力F作用下,从倾角为θ的固定斜面底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则( ) (2013?商丘二模)机械横波某时刻的波形图如图所示,波沿x轴正方向传播,质点p的坐标x=0.32m.从此时刻开始计时.
(2013?商丘二模)机械横波某时刻的波形图如图所示,波沿x轴正方向传播,质点p的坐标x=0.32m.从此时刻开始计时.