题目内容
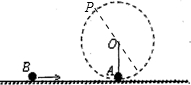
 (2011?重庆模拟)如图所示,光滑绝缘水平面上方有匀强电场E(图中未画出).在O点用长为L的轻质不可伸长的绝缘细绳系一质量m=0.02kg、带正电且电荷量q=4×10-4C的小球A,使其在竖直平面内以速度vA=2m/s沿顺时针方向做匀速圆周运动,运动到最低点时与地面刚好不接触.质量和电量与A完全相同的小球B以速度vB=10m/s 水平向右运动且恰好能与A球在最低点发生正碰,并瞬间成为一个整体C ( A、B、C均可以看作质点且与地面刚好不接触),碰后匀强电场大小立即变为E′=
(2011?重庆模拟)如图所示,光滑绝缘水平面上方有匀强电场E(图中未画出).在O点用长为L的轻质不可伸长的绝缘细绳系一质量m=0.02kg、带正电且电荷量q=4×10-4C的小球A,使其在竖直平面内以速度vA=2m/s沿顺时针方向做匀速圆周运动,运动到最低点时与地面刚好不接触.质量和电量与A完全相同的小球B以速度vB=10m/s 水平向右运动且恰好能与A球在最低点发生正碰,并瞬间成为一个整体C ( A、B、C均可以看作质点且与地面刚好不接触),碰后匀强电场大小立即变为E′=| 3 |
( 1 )匀强电场的电场强度E的大小和方向;
( 2 )A、B两小球正碰成为一个整体C的速度大小;
( 3 )要使整体C在随后的运动过程中,能在竖直面内作完整的圆周运动,绳长L应满足的条件.
分析:(1)对小球受力分析,受到重力、电场力和绳子的拉力,由于小球A在竖直平面内做匀速圆周运动,故重力和电场力做的总功一直为零,故重力和电场力平衡,拉力提供向心力;
(2)根据动量守恒定律列式求解即可;
(3)要使整体C在随后的运动过程中,能在竖直面内作完整的圆周运动,临界条件是通过重力场和电场的复合场的最高点时,重力和电场力的合力恰好提供向心力,然后根据牛顿第二定律、动能定理列方程联立求解.
(2)根据动量守恒定律列式求解即可;
(3)要使整体C在随后的运动过程中,能在竖直面内作完整的圆周运动,临界条件是通过重力场和电场的复合场的最高点时,重力和电场力的合力恰好提供向心力,然后根据牛顿第二定律、动能定理列方程联立求解.
解答:解:(1)小球A在竖直平面内做匀速圆周运动,所以受到的电场力与重力大小相等、方向相反,即有
qE=mg
解得E=500N/C
A球受到的电场力竖直向上,则电场方向竖直向上
即匀强电场的电场强度E的大小为500N/C,方向为竖直向上.
(2)设AB碰撞后瞬间整体C带电量为Q,质量为M,速度为V
Q=2q=8×10-4C,M=2m=0.04kg
由动量守恒,得到 mvA-mvB=MV
解得V=4m/s
即A、B两小球正碰成为一个整体C的速度大小为4m/s.
(3)对C受力情况分析可知:C受电场力和重力的合力为恒力F,大小为F=2Mg,方向与竖直方向夹角为60°,其等效最高点为P点,即PO与竖直方向夹角为60°,F沿着PO方向.
要使整体C在随后的运动过程中,能在竖直面内做完整的圆周运动,需C能通过P点,设绳子对C弹力为T,根据向心力公式,有
F+T=M
T≥0
得到vP≥
C由水平面运动到P点过程,根据动能定理,得到:
-Mg
-QE′
L=
M
-
Mv2
解得:L≤0.2m
即绳子长度L应该满足的条件:0<L≤0.2m.
qE=mg
解得E=500N/C
A球受到的电场力竖直向上,则电场方向竖直向上
即匀强电场的电场强度E的大小为500N/C,方向为竖直向上.
(2)设AB碰撞后瞬间整体C带电量为Q,质量为M,速度为V
Q=2q=8×10-4C,M=2m=0.04kg
由动量守恒,得到 mvA-mvB=MV
解得V=4m/s
即A、B两小球正碰成为一个整体C的速度大小为4m/s.
(3)对C受力情况分析可知:C受电场力和重力的合力为恒力F,大小为F=2Mg,方向与竖直方向夹角为60°,其等效最高点为P点,即PO与竖直方向夹角为60°,F沿着PO方向.

要使整体C在随后的运动过程中,能在竖直面内做完整的圆周运动,需C能通过P点,设绳子对C弹力为T,根据向心力公式,有
F+T=M
| ||
| L |
T≥0
得到vP≥
| 2gL |
C由水平面运动到P点过程,根据动能定理,得到:
-Mg
| 3L |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| v | 2 p |
| 1 |
| 2 |
解得:L≤0.2m
即绳子长度L应该满足的条件:0<L≤0.2m.
点评:本题关键是分析清楚各个小球的运动规律,然后根据牛顿第二定律和动能定理列方程联立求解;难点在于将重力场和电场看作一个复合场进行处理,切入点在于小球恰好通过复合场的最高点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011?重庆模拟)据报道,“嫦娥二号”探月卫星于2010年10月1日18时59分57秒在西昌卫星中心发射,其环月飞行的高度距离月球表面100km,所探测到有关月球的数据将比环月飞行高度为200km.的嫦娥一号更加详实,已知月球表面的重力加速度约为地球表面重力加速度的
(2011?重庆模拟)据报道,“嫦娥二号”探月卫星于2010年10月1日18时59分57秒在西昌卫星中心发射,其环月飞行的高度距离月球表面100km,所探测到有关月球的数据将比环月飞行高度为200km.的嫦娥一号更加详实,已知月球表面的重力加速度约为地球表面重力加速度的 (2011?重庆模拟)如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大一些,应该采取的措施是( )
(2011?重庆模拟)如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大一些,应该采取的措施是( ) (2011?重庆模拟)如图所示,是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,c点为此时刻即将开始振动的点,该波速度为40m/s.下列说法中正确的是( )
(2011?重庆模拟)如图所示,是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,c点为此时刻即将开始振动的点,该波速度为40m/s.下列说法中正确的是( )