题目内容
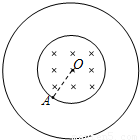
图示为两个共轴金属圆筒,轴线与纸面垂直,内筒半径为R,筒壁为网状(带电粒子可无阻挡地穿过网格)。当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向的电场。内圆筒包围的空间存在一沿圆筒轴线方向的匀强磁场,磁场的磁感应强度的大小为B,方向指向纸内。一束质量为m、电量为q的带正电的粒子以各种不同的速率自内圆筒壁上的A点沿内圆筒半径射入磁场,现要求有的粒子的运动能满足下面三个条件:①刚刚能到达外筒的内壁而不与外筒相碰;②粒子恰能从A点射出磁场;③每个粒子在磁场区域内运动所经过的总时间等于该粒子在所给磁场中做完整的圆周运动时的周期的一半。
(1)为了能满足上述要求,内、外筒间电压的可能值应是多少?
(2)讨论上述电压取最小值时,粒子在磁场中的运动情况。
(1) ![]() k = 1, 2, 3, … (2)
k = 1, 2, 3, … (2) ![]()
解析:
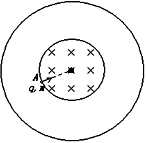
[1] 设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,并从内筒表面上的A1点射出磁场,射出磁场时的速度大小仍为v,方向沿过A1点的内圆筒半径方向,如图所示。粒子自A1射出磁场后便进入两圆筒间的电场中,在电场力的作用下,粒子做减速直线运动,刚到达外圆筒的内壁时,速度恰好减至零。然后粒子又在电场力作用下向A1点做加速运动,回到时,粒子速度增大到v,并以此速度沿圆筒内圆半径方向第二次进入磁场,在磁场的洛仑兹力作用下,粒子又做圆周运动,并从A2点射出磁场。此后,粒子又再一次在电场中减速,到达外壁时调转方向加速回到A2点,从A2点进入磁场,再做圆周运动并从A3点射出磁场。这一过程多次重复到最后,粒子再次从A点射出磁场。
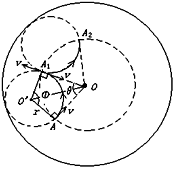
设粒子做圆周运动的半径为r,从A点射入磁场到从A1点射出磁场经历的时间为t,绕圆心o’转过的角度为Ф,过A点和A1点的内圆筒半径对其轴线o的张角为θ,如图所示。有
![]() ⑴
⑴
![]() ⑵
⑵
若粒子在磁场中经过n次偏转后能从A点射出磁场,应满足条件nθ = 2kπ ⑶
根据题意有 ![]() ⑷
⑷
而 ![]() ⑸
⑸
解以上各式得n = 2k+1 k = 1, 2, 3, … ⑹
![]() k = 1, 2, 3, … ⑺
k = 1, 2, 3, … ⑺
连结图中的oo’,由直角三角形Aoo’可得: ![]() ⑻
⑻
因r是粒子在洛仑兹力作用下做圆周运动的轨道半径,有![]() ⑼
⑼
由⑵、⑻、⑼式得到粒子射入磁场时的速度![]() ⑽
⑽
设加在两圆筒间的电压为U,由能量守恒有![]() ⑾
⑾
把⑽式代入⑾式得![]() k = 1, 2, 3, … ⑿
k = 1, 2, 3, … ⑿
[2] 当k=1时,对应射入磁场的速度为最小,加在两圆筒间的电压亦为最小,
![]() ⒀
⒀
![]() ⒁
⒁
由⑹式可知粒子在磁场中偏转的次数为 n = 3 ⒂
由⑺式可知每次偏转的角度 θ3 = 120° ⒃
由⑻式和⑺可知粒子在磁场内做圆周运动的半径 ![]() ⒄
⒄
粒子在磁场内运动的总路程 ![]() ⒅
⒅

 如图所示:为两个共轴金属圆筒,轴线与纸面垂直,内筒半径为R,筒壁为网状(带电粒子可无阻挡地穿过网格).当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向的电场.内圆筒包围的空间存在一沿圆筒轴线方向的匀强磁场,磁场的磁感应强度的大小为B,方向指向纸内.一束质量为m、电量为q的带正电的粒子以各种不同的速率自内圆筒壁上的A点沿内圆筒半径射入磁场,现要求有的粒子的运动能满足下面三个条件:①刚刚能到达外筒的内壁而不与外筒相碰;②粒子恰能从A点射出磁场;③每个粒子在磁场区域内运动所经过的总时间等于该粒子在所给磁场中做完整的圆周运动时的周期的一半.
如图所示:为两个共轴金属圆筒,轴线与纸面垂直,内筒半径为R,筒壁为网状(带电粒子可无阻挡地穿过网格).当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向的电场.内圆筒包围的空间存在一沿圆筒轴线方向的匀强磁场,磁场的磁感应强度的大小为B,方向指向纸内.一束质量为m、电量为q的带正电的粒子以各种不同的速率自内圆筒壁上的A点沿内圆筒半径射入磁场,现要求有的粒子的运动能满足下面三个条件:①刚刚能到达外筒的内壁而不与外筒相碰;②粒子恰能从A点射出磁场;③每个粒子在磁场区域内运动所经过的总时间等于该粒子在所给磁场中做完整的圆周运动时的周期的一半. 如图所示,两个共轴金属圆筒轴线O与纸面垂直,内筒筒壁为网状(带电粒子可无阻挡地穿过网格),半径为R.内圆筒包围的空间存在一沿圆筒轴线方向指向纸内的匀强磁场,磁场的磁感应强度的大小为B.当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向这指向轴线的电场.一束质量为m、电量为q的带正电的粒子自内圆筒壁上的A点沿内圆筒半径射入磁场,经磁场偏转进入电场后所有粒子都刚好不与外筒相碰.试问:
如图所示,两个共轴金属圆筒轴线O与纸面垂直,内筒筒壁为网状(带电粒子可无阻挡地穿过网格),半径为R.内圆筒包围的空间存在一沿圆筒轴线方向指向纸内的匀强磁场,磁场的磁感应强度的大小为B.当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向这指向轴线的电场.一束质量为m、电量为q的带正电的粒子自内圆筒壁上的A点沿内圆筒半径射入磁场,经磁场偏转进入电场后所有粒子都刚好不与外筒相碰.试问: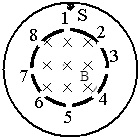 如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.
如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.