题目内容
如图所示,两个共轴金属圆筒轴线O与纸面垂直,内筒筒壁为网状(带电粒子可无阻挡地穿过网格),半径为R.内圆筒包围的空间存在一沿圆筒轴线方向指向纸内的匀强磁场,磁场的磁感应强度的大小为B.当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向这指向轴线的电场.一束质量为m、电量为q的带正电的粒子自内圆筒壁上的A点沿内圆筒半径射入磁场,经磁场偏转进入电场后所有粒子都刚好不与外筒相碰.试问:(1)要使粒子在最短时间内再次到达A点,粒子的速度应是多少?再次到达A点在磁场中运动的最短时间是多长?
(2)要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,则内、外筒之间的电压需满足什么条件?
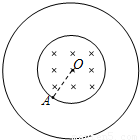
【答案】分析:(1)设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,并从内筒表面上的A1点射出磁场,射出磁场时的速度大小仍为v,方向沿过A1点的内圆筒半径方向,如图所示.粒子自A1射出磁场后便进入两圆筒间的电场中,在电场力的作用下,粒子做减速直线运动,刚到达外圆筒的内壁时,速度恰好减至零.然后粒子又在电场力作用下向A1点做加速运动,回到时,粒子速度增大到v,并以此速度沿圆筒内圆半径方向第二次进入磁场,在磁场的洛仑兹力作用下,粒子又做圆周运动,并从A2点射出磁场.此后,粒子又再一次在电场中减速,到达外壁时调转方向加速回到A2点,从A2点进入磁场,再做圆周运动并从A3点射出磁场.这一过程多次重复到最后,粒子再次从A点射出磁场.要使粒子在最短时间内再次到达A点,轨迹对应的圆心角最小,且在磁场中旋转的次数最少,可知,粒子进入电场两次,根据轨迹的形状和几何知识求出轨迹的半径,由牛顿第二定律求解速度,根据轨迹的圆心角求时间.
(2)要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,设粒子进入电场共n次,由几何知识求出轨迹半径,由牛顿第二定律求得其速率,再根据动能定理求出电压应满足的条件.
解答:解:(1)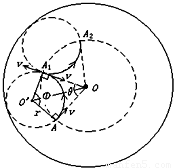 设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,当粒子第三次进入磁场时,轨迹对应的圆心角最小,所用时间最短,由几何知识得:此时轨迹的圆心角φ=180°-120°=60°
设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,当粒子第三次进入磁场时,轨迹对应的圆心角最小,所用时间最短,由几何知识得:此时轨迹的圆心角φ=180°-120°=60°
则轨迹半径为 r=Rtan60°=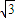 R
R
根据牛顿第二定律得:qvB=m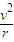
联立解得,v=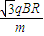
运动的最短时间为tmin=3× T=
T=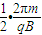 =
=
(2)设粒子做圆周运动的半径为r,从A点射入磁场到从A1点射出磁场绕圆心o’转过的角度为Ф,过A点和A1点的内圆筒半径对其轴线o的张角为θ,如图所示.有 Φ+θ=π ①
要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,若粒子在磁场中经过n次偏转后能从A点射出磁场,应满足条件nθ=2π ②(n=3,4,5…)
解得θ=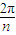 ③
③
连结图中的OO′,由直角三角形AOO′可得:tan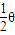 =
=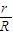 ④
④
因r是粒子在洛仑兹力作用下做圆周运动的轨道半径,有r=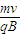 ⑤
⑤
由③④⑤式得到粒子射入磁场时的速度v=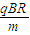 tan
tan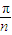 ⑥
⑥
设加在两圆筒间的电压为U,由能量守恒有
qU=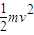 ⑦
⑦
由⑥⑦解得,U=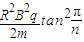 (n=3,4,5…)
(n=3,4,5…)
答:
(1)要使粒子在最短时间内再次到达A点,粒子的速度应是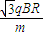 ,再次到达A点在磁场中运动的最短时间是
,再次到达A点在磁场中运动的最短时间是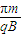 .
.
(2)要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,则内、外筒之间的电压需满足条件是U=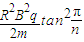 (n=3,4,5…).
(n=3,4,5…).
点评:本题是有界磁场的问题,要充分运用几何知识画出轨迹、分析和求解轨迹半径和圆心角,考查运用数学知识解决物理问题的能力,难度较大.
(2)要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,设粒子进入电场共n次,由几何知识求出轨迹半径,由牛顿第二定律求得其速率,再根据动能定理求出电压应满足的条件.
解答:解:(1)
 设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,当粒子第三次进入磁场时,轨迹对应的圆心角最小,所用时间最短,由几何知识得:此时轨迹的圆心角φ=180°-120°=60°
设带电粒子自A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛仑兹力作用下粒子做圆周运动,当粒子第三次进入磁场时,轨迹对应的圆心角最小,所用时间最短,由几何知识得:此时轨迹的圆心角φ=180°-120°=60°则轨迹半径为 r=Rtan60°=
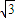 R
R根据牛顿第二定律得:qvB=m
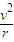
联立解得,v=
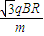
运动的最短时间为tmin=3×
 T=
T=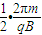 =
=
(2)设粒子做圆周运动的半径为r,从A点射入磁场到从A1点射出磁场绕圆心o’转过的角度为Ф,过A点和A1点的内圆筒半径对其轴线o的张角为θ,如图所示.有 Φ+θ=π ①
要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,若粒子在磁场中经过n次偏转后能从A点射出磁场,应满足条件nθ=2π ②(n=3,4,5…)
解得θ=
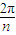 ③
③连结图中的OO′,由直角三角形AOO′可得:tan
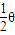 =
=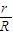 ④
④因r是粒子在洛仑兹力作用下做圆周运动的轨道半径,有r=
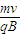 ⑤
⑤由③④⑤式得到粒子射入磁场时的速度v=
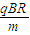 tan
tan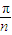 ⑥
⑥设加在两圆筒间的电压为U,由能量守恒有
qU=
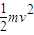 ⑦
⑦由⑥⑦解得,U=
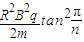 (n=3,4,5…)
(n=3,4,5…)答:
(1)要使粒子在最短时间内再次到达A点,粒子的速度应是
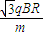 ,再次到达A点在磁场中运动的最短时间是
,再次到达A点在磁场中运动的最短时间是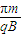 .
.(2)要使粒子在磁场中围绕圆筒的轴线O运动一周时恰能返回A点,则内、外筒之间的电压需满足条件是U=
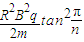 (n=3,4,5…).
(n=3,4,5…).点评:本题是有界磁场的问题,要充分运用几何知识画出轨迹、分析和求解轨迹半径和圆心角,考查运用数学知识解决物理问题的能力,难度较大.

练习册系列答案
相关题目
 如图所示,两个共轴金属圆筒轴线O与纸面垂直,内筒筒壁为网状(带电粒子可无阻挡地穿过网格),半径为R.内圆筒包围的空间存在一沿圆筒轴线方向指向纸内的匀强磁场,磁场的磁感应强度的大小为B.当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向这指向轴线的电场.一束质量为m、电量为q的带正电的粒子自内圆筒壁上的A点沿内圆筒半径射入磁场,经磁场偏转进入电场后所有粒子都刚好不与外筒相碰.试问:
如图所示,两个共轴金属圆筒轴线O与纸面垂直,内筒筒壁为网状(带电粒子可无阻挡地穿过网格),半径为R.内圆筒包围的空间存在一沿圆筒轴线方向指向纸内的匀强磁场,磁场的磁感应强度的大小为B.当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向这指向轴线的电场.一束质量为m、电量为q的带正电的粒子自内圆筒壁上的A点沿内圆筒半径射入磁场,经磁场偏转进入电场后所有粒子都刚好不与外筒相碰.试问:

