题目内容
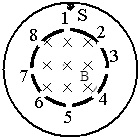 如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.
如图,两个共轴的圆筒形金属电极,在内筒上均匀分布着平行于轴线的标号1-8的八个狭缝,内筒内半径为R,在内筒之内有平行于轴线向里的匀强磁场,磁感应强度为B.在两极间加恒定电压,使筒之间的区域内有沿半径向里的电场.不计粒子重力,整个装置在真空中,粒子碰到电极时会被电极吸收.(1)一质量为m1,带电量为+q1的粒子从紧靠外筒且正对1号缝的S点由静止出发,进入磁场后到达的第一个狭缝是3号缝,求两电极间加的电压U是多少?
(2)另一个粒子质量为m2,带电量为+q2,也从S点由静止出发,该粒子经过一段时间后恰好又回到S点,求该粒子在磁场中运动多少时间第一次回到S点.
分析:(1)带电粒子从S点出发,在两筒之间的电场作用下加速,沿径向穿过狭缝a而进入磁场区,在洛伦兹力作用下做匀速圆周运动.粒子从1号缝直接到3号缝,轨迹为
圆周,轨迹半径等于内筒半径,由牛顿第二定律列式求出速度,由根据动能定理求出加速电压.
(2)粒子再回到S点的条件是能沿径向穿过狭缝,只要穿过了狭缝,粒子就会在电场力作用下先减速,再反向加速,再重新进入磁场区,再回到S点.画出粒子可能的运动轨迹,共有三种可能情况:第一种:粒子依次经过2、3、4、5、6、7、8号缝回到1号缝;第二种:粒子依次经3、5、7号缝回到1号缝;第三种:粒子依次经过4、7、2、5、8、3、6号缝回到1号缝.确定出轨迹的圆心角,求出总时间.
| 1 |
| 4 |
(2)粒子再回到S点的条件是能沿径向穿过狭缝,只要穿过了狭缝,粒子就会在电场力作用下先减速,再反向加速,再重新进入磁场区,再回到S点.画出粒子可能的运动轨迹,共有三种可能情况:第一种:粒子依次经过2、3、4、5、6、7、8号缝回到1号缝;第二种:粒子依次经3、5、7号缝回到1号缝;第三种:粒子依次经过4、7、2、5、8、3、6号缝回到1号缝.确定出轨迹的圆心角,求出总时间.
解答:解:(1)m1粒子从S点出发在电场力作用下加速沿径向由1号缝以速度V1进入磁场,
依动能定理 q1U=
mV12 ①
在磁场中做匀速圆周运动,由洛伦兹力公式和牛顿定律得 qV1B=m
②
粒子从1号缝直接到3号缝,轨迹为1/4圆周,轨迹半径等于内筒半径r1=R ③
由以上得 U=
④
(2)m2粒子进入磁场后,做匀速圆周运动周期为T qv2B=m2
⑤
周期为 T=
⑥
得 T=
⑦
m2粒子能回到S点的条件是能沿径向进入某条缝,在电场中先减速再反向加速重回磁场,然后以同样的方式经过某些缝最后经1号缝回到S点.共有三种可能情况
第一种:粒子依次经过2、3、4、5、6、7、8号缝回到1号缝.

t=8×
×T=3T=
⑧
第二种:粒子依次经3、5、7号缝回到1号缝 t=4×
T=T=
⑨
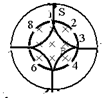
第三种:粒子依次经过4、7、2、5、8、3、6号缝回到1号缝 t=8×
T=T=
⑩

答:(1)两电极间加的电压U是
.
(2)另一个粒子质量为m2,带电量为+q2,也从S点由静止出发,该粒子经过一段时间后恰好又回到S点,该粒子在磁场中第一次回到S点的运动时间可能为:
或
.
依动能定理 q1U=
| 1 |
| 2 |
在磁场中做匀速圆周运动,由洛伦兹力公式和牛顿定律得 qV1B=m
| V12 |
| r1 |
粒子从1号缝直接到3号缝,轨迹为1/4圆周,轨迹半径等于内筒半径r1=R ③
由以上得 U=
| q1R2B2 |
| 2m1 |
(2)m2粒子进入磁场后,做匀速圆周运动周期为T qv2B=m2
| v22 |
| r2 |
周期为 T=
| 2πr2 |
| v2 |
得 T=
| 2πm2 |
| q2B |
m2粒子能回到S点的条件是能沿径向进入某条缝,在电场中先减速再反向加速重回磁场,然后以同样的方式经过某些缝最后经1号缝回到S点.共有三种可能情况
第一种:粒子依次经过2、3、4、5、6、7、8号缝回到1号缝.

t=8×
| 135 |
| 360 |
| 6πm2 |
| q2B |
第二种:粒子依次经3、5、7号缝回到1号缝 t=4×
| 1 |
| 4 |
| 2πm2 |
| q2B |

第三种:粒子依次经过4、7、2、5、8、3、6号缝回到1号缝 t=8×
| 1 |
| 8 |
| 2πm2 |
| q2B |

答:(1)两电极间加的电压U是
| q1R2B2 |
| 2m1 |
(2)另一个粒子质量为m2,带电量为+q2,也从S点由静止出发,该粒子经过一段时间后恰好又回到S点,该粒子在磁场中第一次回到S点的运动时间可能为:
| 6πm2 |
| q2B |
| 2πm2 |
| q2B |
点评:本题看似较为复杂,实则简单; 带电粒子在磁场运动解决的关键在于要先明确粒子可能的运动轨迹,只要能确定圆心和半径即可由牛顿第二定律及向心力公式求得结果.

练习册系列答案
相关题目
 (2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)
(2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)

