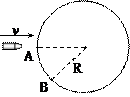题目内容
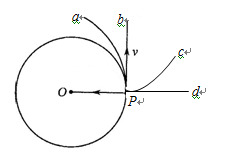
如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速运动（图示为截面）。从枪口发射的子弹沿直径穿过圆筒。若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度。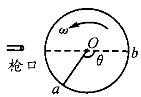
v=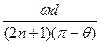
（n=0，1，2，…）
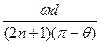（n=0，1，2，…）设子弹速度为v，则子弹穿过筒的时间 t=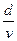
此时间内筒转过的角度 α=π—θ
据α=ωt，得 π一θ=ω，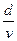
则子弹速度 v=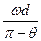
本题中若无角度的限制，则在时间t内转过的角度 α=2nπ+π一θ=π（2n+1）一θ
α=2nπ十π一θ=π（2n+1）一θ
则子弹速度 v=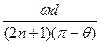（n=0，1，2，…）
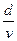
此时间内筒转过的角度 α=π—θ
据α=ωt，得 π一θ=ω
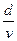，则子弹速度 v=
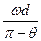
本题中若无角度的限制，则在时间t内转过的角度 α=2nπ+π一θ=π（2n+1）一θ
α=2nπ十π一θ=π（2n+1）一θ
则子弹速度 v=
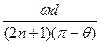（n=0，1，2，…） 
练习册系列答案
相关题目
L，B处绳长为L，两根绳能承受的最大拉力均为2mg，转轴带动小球转动。则：
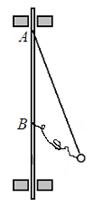
多大？
